Treasury Yield Premiums
The Treasury yield premium model by Jens H.E. Christensen and Glenn D. Rudebusch (CR) decomposes the nominal yield curve into three components: future short-term interest rate expectations, a term premium that measures bond investor aversion to the risk of holding longer-maturity bonds, and a model residual. It is important to note that the CR model is Gaussian and does not enforce a zero lower bound on nominal yields.
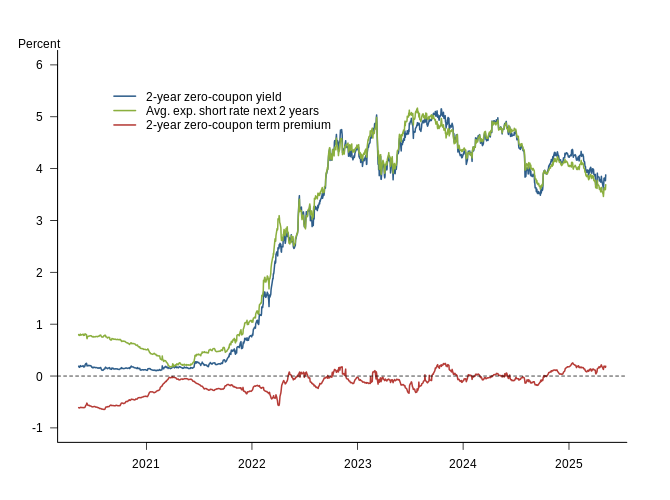
The two-year Treasury yield decomposition divides the two-year zero-coupon nominal Treasury yield into the average expected short rate over the next two years and the associated two-year term risk premium. The unexplained model residual is included in the term premium so that the two components add up to the observed Treasury yield.
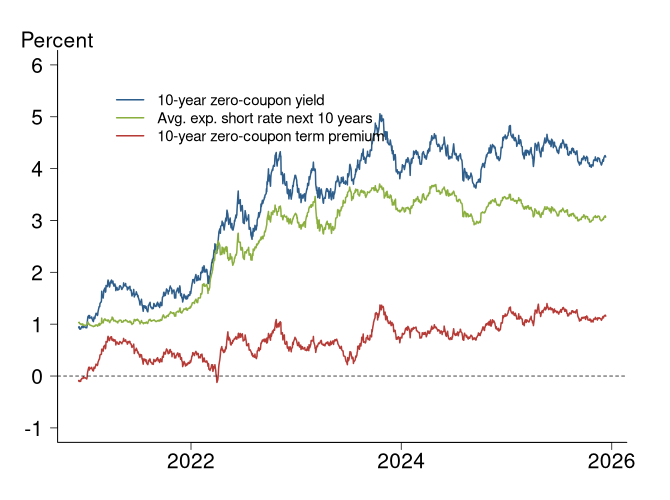
The 10-year Treasury yield decomposition divides the 10-year zero-coupon nominal Treasury yield into the average expected short rate over the next 10 years and the associated 10-year term risk premium. The unexplained model residual is included in the term premium so that the two components add up to the observed Treasury yield.
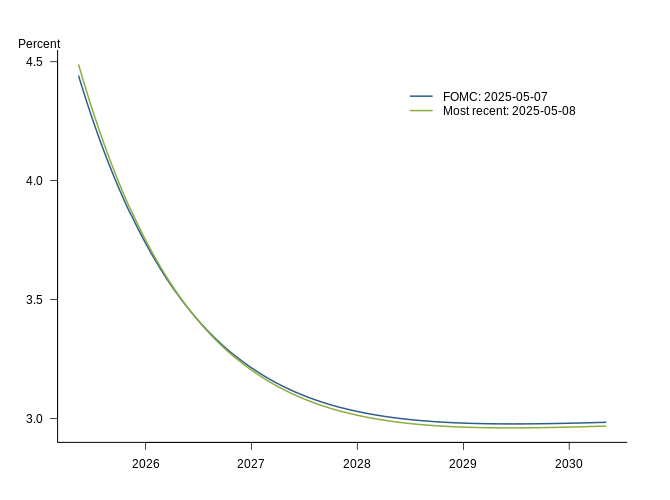
The estimated short rate path is the expected path for the short-term interest rate priced into the nominal Treasury yield curve after accounting for bond risk premiums. It is the measure relevant for macroeconomic and monetary policy analysis as well as risk management. Shown is the CR model-implied short rate path for the latest model estimates along with the rate path on the last day of the most recent FOMC meeting.
Decomposition of Treasury Yields
| Policy Expectations and Term Premiums | Most Recent | Last FOMC | 1 year ago |
|---|---|---|---|
| (2024-04-22) | (2024-03-20) | (2023-04-25) | |
| Treasury Yield (Observed) | |||
| 2-year | 4.9 | 4.56 | 4.23 |
| 10-year | 4.59 | 4.28 | 3.63 |
| Average Expected Overnight Rate | |||
| 2-year | 4.88 | 4.62 | 4.27 |
| 10-year | 3.67 | 3.44 | 3.01 |
| Term Premium | |||
| 2-year | 0.03 | -0.05 | -0.04 |
| 10-year | 0.92 | 0.84 | 0.62 |
Data and Estimation Details
The model is a three-factor, affine Gaussian term structure model centered around the affine arbitrage-free class of Nelson-Siegel (AFNS) term structure models derived in Christensen, Diebold, and Rudebusch (2011). The model’s objective dynamics are identical to those of the U.S. AFNS model favored by Christensen and Rudebusch (2012).
The data used in the estimation consist of daily off-the-run, nominal Treasury zero-coupon bond yields from the Gürkaynak-Sack-Wright (2007) database with eight constant maturities (3-month, 6-month, 1-year, 2-year, 3-year, 5-year, 7-year, and 10-year) covering the period from December 1, 1987, until the present.
The CR model is estimated with the standard Kalman filter, which is a consistent and efficient estimator in this setting. The model has been re-estimated daily going back to January 2, 1998. As a consequence, each term premium estimate since then only contains information available up to the time of the estimate.
References
Christensen, Jens H.E., Francis X. Diebold, and Glenn D. Rudebusch. 2011. “The Affine Arbitrage-Free Class of Nelson-Siegel Term Structure Models.” Journal of Econometrics 164(1), pp. 4-20.
Christensen, Jens H.E., and Glenn D. Rudebusch. 2012. “The Response of Interest Rates to U.S. and U.K. Quantitative Easing.” Economic Journal 122, pp. F385-F414.
Gürkaynak, Refet S., Brian Sack, and Jonathan H. Wright. 2007. “The U.S. Treasury Yield Curve: 1961 to the Present.” Journal of Monetary Economics 54(8), pp. 2,291-2,304.
Download Data
Website Chart Data (Excel document, 380 kb)
Complete Model Data (Excel document, 3.5 mb)
Contact Jens.Christensen (at) sf.frb.org


