This Economic Letter discusses a topic that at first glance appears to be boring and technical but that in fact turns out to be quite important: the proper interpretation of chain-weighted data. To illustrate, consider this simple question: What is the growth rate of real GDP?
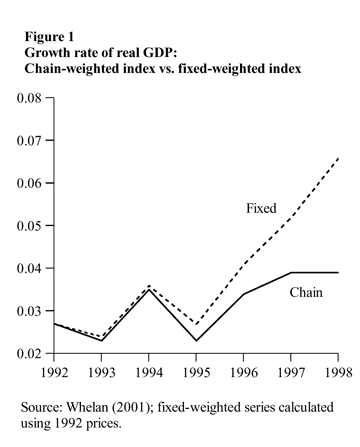
This Economic Letter discusses a topic that at first glance appears to be boring and technical but that in fact turns out to be quite important: the proper interpretation of chain-weighted data. To illustrate, consider this simple question: What is the growth rate of real GDP? Figure 1 displays two different answers to this question for the period 1992 to 1998. The solid line is calculated using a chain-weighted index, the method currently used by the U.S. Department of Commerce in the National Income and Product Accounts (NIPA); the dashed line is calculated using a fixed-weighted index, the method NIPA statisticians used up to 1997. According to the chain-weighted measure, the growth rate of real GDP rose to just under 4% by 1997 and 1998. Although this was relatively rapid compared to the growth rates observed earlier in the decade, it pales in comparison to the growth rate calculated using a fixed-weighted measure, which rises sharply after 1995, reaching a rate of 6.6% by 1998. By this measure, the “New Economy” of the late 1990s looks even more remarkable!
Which growth measure is right, and why are the two rates different? This Economic Letter attempts to answer these questions and to draw out their implications for interpreting and using NIPA data.
Why chain weights are preferred
A fundamental issue in comparing GDP this year with GDP in years past is determining how much of any increase is real and how much reflects price inflation. A natural way to control for price inflation is to value GDP in both periods using the same, constant set of prices. This is exactly what the fixed-weighted GDP measure does: GDP is valued at a common basket of prices, say 1992 prices, and the resulting estimates are called GDP in “constant 1992 dollars.”
The problem with this approach is that the measure of real GDP becomes less and less accurate as one moves further away from the base year; as Figure 1 illustrates, in constant 1992 dollars, the growth rate of fixed-weighted GDP increasingly overstates the “true” chain-weighted growth rate of real GDP. The reason is that the components of GDP that grow fastest tend to be those that exhibit the smallest price increases, or even price declines, so the fixed-weighted real GDP measure tends to weight these components more heavily than later prices would suggest.
To see how this happens, consider an economy consisting of just two sectors—computers and oranges—and whose consumers spend half their income on computers and half their income on oranges each year. Now suppose that productivity growth in the computer sector is a very rapid 10% per year, while productivity growth in the orange sector is zero, so that each year the economy produces 10% more computers and a constant number of oranges. In such an economy, the price of computers relative to the price of oranges declines over time.
To construct a real fixed-weighted GDP using prices from, say, Year 1 of the economy, we sum the number of computers produced and the number of oranges produced in every year, weighted by their fixed prices. Since the number of computers is growing rapidly while the number of oranges is fixed, the growth rate of the fixed-weighted GDP rises over time, eventually approaching 10% per year, the growth rate of computers. In this example, the contribution of oranges to GDP essentially disappears, even though consumers always spend half their (nominal) income on oranges.
The chain-weighted measure of real GDP solves this problem by updating the weights in every period. For example, the growth rate between 1992 and 1993 is computed using prices that prevailed in 1992 and 1993, while the growth rate between 1997 and 1998 is computed using prices that prevailed in 1997 and 1998. What happens if we apply the chain-weighted approach in the computers-oranges example? Although the result depends on some rather complicated mathematics that is beyond the scope of this Letter, it is nonetheless intuitive: the growth rate of real GDP is simply a weighted average of the growth rates of the two sectors, where the weights are the expenditure shares, equal to 1/2 in our example. Therefore the growth rate of real chain-weighted GDP in this example is constant over time and equals 1/2 the growth rate in the computer sector, or 5%. Intuitively, this more accurately reflects what is going on in our simple economy than the fixed-weighted measure. Since 1997, these chain-weighted measures have been reported in the NIPA data, and one rarely encounters the fixed-weighted measures.
Not surprisingly, similar measurement issues arise at the industry level. For example, according to fixed-weighted measures based on 1987 prices, the manufacturing sector grew at a rate of 1.7% per year between 1977 and 1987. In contrast, using the more accurate chain-weighting, the average annual growth rate over this period was a full percentage point higher at 2.7% (Landefeld and Parker 1997).
If the chain-weighted measures are preferred and the fixed-weighted measures are no longer reported, then what is there to be careful about? It turns out that one of the main advantages of the fixed-weighted measures of real GDP is lost: fixed-weighted measures are additive, but chain-weighted measures are not. Nominal GDP is equal to the sum of consumption, investment, government purchases, and net exports. The same thing is true with a fixed-weight measure of real GDP. However, it is not true of the chain-weighted indexes for real GDP and its components: real GDP does not generally equal the sum of real consumption, real investment, real government expenditures, and real net exports.
To get an intuition about why this is so, we can return to the computers-oranges economy. Chain-weighted calculations start the same way as fixed-weighted calculations do, namely, by picking a reference year (current 1996 in the NIPA data) and setting that year’s real GDP equal to that year’s nominal GDP. The level in subsequent years is computed by successively applying the chain growth rate—here equal to 5%—to the level in the reference year. The same method applies to the other components of GDP, real computer output and real orange output. In the reference year, by construction, the real chain-weighted outputs sum to equal GDP because all are equal to their nominal counterparts. But since real computer output grows at 10% per year while real orange output is constant, these outputs do not add up to real GDP in any subsequent year; in fact, they suffer the same problem as a fixed-weighted index in that the sum of the real outputs will eventually be dominated by the computer sector and grow at a rate of 10% per year.
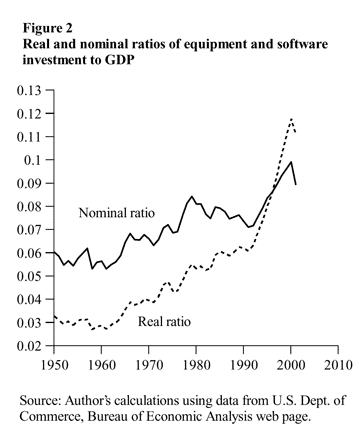
An important problem that arises from this lack of additivity is in calculating shares of output. For example, one might naturally wonder how the share of equipment and software investment in GDP has changed over time. Two candidates for this share are plotted in Figure 2. One is constructed by dividing nominal equipment and software investment by nominal GDP. The other is constructed by dividing real equipment and software investment by real GDP. Obviously, the two measures look quite different: the nominal ratio has grown from about 6% in 1950 to about 10% in 2000, while the real ratio has grown from about 3% in 1950 to nearly 12% in 2000. Which series is correct?
The difference between the two series is a relative price: the price index for equipment and software divided by the price index for GDP. This price has been declining very rapidly over this period, in large part reflecting the rapid productivity growth in semiconductor production. Because nominal GDP is additive, the nominal ratio is a true “share”—it must lie between zero and one. However, because real chain-weighted GDP is not additive, there is no reason for this real ratio to be between zero and one. In fact, if the rapid productivity growth in semiconductors continues, one can imagine that someday this ratio will exceed one. In this case, then, the nominal share is more informative. The lesson from this example is that one must be very careful in using ratios and sums of the components of real GDP because these series lack additivity.
The use of chain-weights instead of fixed-weights in the NIPA data is a significant step forward. It should provide policymakers, forecasters, and businesses with a more accurate picture of economic growth. Nevertheless, this more accurate picture does come at a cost: the chain-weighted data are not additive, and this means that interpreting and using the NIPA data require additional care.
Charles I. Jones
Associate Professor, UC Berkeley,
and Visiting Scholar, FRBSF
Landefeld, J. Steven, and Robert P. Parker. 1997. “BEA’s Chain Indexes, Time Series, and Measures of Long-Term Economic Growth.” Survey of Current Business (May) pp. 58-68.
Recommended reading
Department of Commerce. Bureau of Economic Analysis. “National Income and Product Accounts Tables.”
Whelan, Karl. 2000. “A Guide to the Use of Chain Aggregated NIPA Data.” Mimeo. Federal Reserve Board of Governors (June).
Whelan, Karl. 2001. “A Two-Sector Approach to Modeling U.S. NIPA Data.” Mimeo. Federal Reserve Board of Governors (April).
Opinions expressed in FRBSF Economic Letter do not necessarily reflect the views of the management of the Federal Reserve Bank of San Francisco or of the Board of Governors of the Federal Reserve System. This publication is edited by Anita Todd and Karen Barnes. Permission to reprint portions of articles or whole articles must be obtained in writing. Please send editorial comments and requests for reprint permission to research.library@sf.frb.org