A recent front-page article in the Wall Street Journal documented an increasing tendency among economists to move away from theories of efficient stock market valuation in favor of “behavioral” models that emphasize the role of irrational investors (see Hilsenrath 2004). The long-run rate of return on stocks is ultimately determined by the stream of corporate earnings distributions (cash flows) that accrue to shareholders.
- Stock as a “disguised bond”
- Long-run yield comparison
- Changing risk perceptions
- Inflation-induced valuation errors
- Conclusion
- References
A recent front-page article in the Wall Street Journal documented an increasing tendency among economists to move away from theories of efficient stock market valuation in favor of “behavioral” models that emphasize the role of irrational investors (see Hilsenrath 2004). The long-run rate of return on stocks is ultimately determined by the stream of corporate earnings distributions (cash flows) that accrue to shareholders. In assigning prices to stocks, efficient valuation theory says that rational investors should discount real cash flows using real interest rates or discount nominal cash flows using nominal interest rates. Twenty-five years ago, Modigliani and Cohn (1979) put forth the hypothesis that investors may irrationally discount real cash flows using nominal interest rates—a behavioral trait that would lead to inflation-induced valuation errors. This Economic Letter examines some recent research that finds support for the Modigliani-Cohn hypothesis. In particular, studies show that the Standard & Poor’s (S&P) 500 stock index tends to be undervalued during periods of high expected inflation (such as the late 1970s and early 1980s) and overvalued during periods of low expected inflation (such as the late 1990s and early 2000s). This result implies that the long bull market that began in 1982 can be partially attributed to the stock market’s shift from a state of undervaluation to one of overvaluation. Going forward, the return on stocks could be influenced by a shift in the opposite direction.
Famed investor Warren Buffett has described a stock as a type of “disguised bond.” A stock represents a claim to a stream of earnings distributions, whereas a bond represents a claim to a stream of coupon payments. Given that stocks and bonds can be viewed as competing assets in a portfolio, investors may wish to compare the valuations of these two asset classes in some quantitative way. Wall Street practitioners typically compare the earnings yield on stocks (denoted here by the E/P ratio, the inverse of the price-earnings ratio) with the nominal yield on a long-term U.S. Treasury bond. Stocks are supposedly undervalued relative to bonds when the E/P ratio exceeds the nominal bond yield and supposedly overvalued relative to bonds when the E/P ratio is below the nominal bond yield. This valuation technique is often referred to as the “Fed model,” but it is important to note that the Federal Reserve neither uses nor endorses it. Many authors, including Ritter and Warr (2002) and Asness (2003), have pointed out that the practice of comparing a real number like the E/P ratio to a nominal yield does not make sense. While it would be more correct to compare the E/P ratio to a real bond yield, that comparison still ignores the different risk characteristics of stocks versus bonds and the reality that, over the past four decades, cash distributions to shareholders in the form of dividends have averaged only about 50% of earnings.
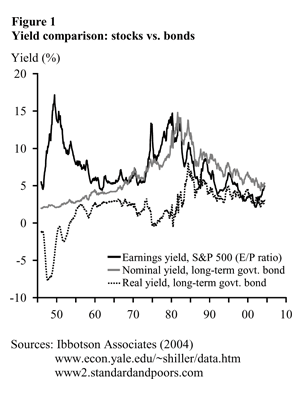 Wall Street practitioners often argue that comparing the E/P ratio to a nominal bond yield is justified by the observed comovement of the two series in the data. Figure 1 plots the E/P ratio of the S&P 500 index (based on 12-month trailing reported earnings) together with the nominal and real yields on a long-term U.S. Treasury bond (with a maturity near 20 years). The figure uses monthly data from December 1945 to June 2004. The real yield is obtained by subtracting expected inflation from the nominal yield. Expected inflation is constructed as an exponentially weighted moving average of past (12-month) CPI inflation, where the weighting scheme is set to approximate the time-series behavior of the one-year-ahead inflation forecast from the Survey of Professional Forecasters.
Wall Street practitioners often argue that comparing the E/P ratio to a nominal bond yield is justified by the observed comovement of the two series in the data. Figure 1 plots the E/P ratio of the S&P 500 index (based on 12-month trailing reported earnings) together with the nominal and real yields on a long-term U.S. Treasury bond (with a maturity near 20 years). The figure uses monthly data from December 1945 to June 2004. The real yield is obtained by subtracting expected inflation from the nominal yield. Expected inflation is constructed as an exponentially weighted moving average of past (12-month) CPI inflation, where the weighting scheme is set to approximate the time-series behavior of the one-year-ahead inflation forecast from the Survey of Professional Forecasters.
The figure shows that the E/P ratio is more strongly correlated with movements in the nominal yield than with the real yield, particularly since the mid-1960s. This result is a puzzle from the perspective of efficient valuation theory. Observed movements in the nominal yield can be largely attributed to changes in expected inflation which, in turn, have been driven by changes in actual inflation. If investors were rationally discounting future nominal cash flows using nominal interest rates, they would understand that inflation-induced changes in the nominal bond yield are accompanied by inflation-induced changes in the magnitude of future nominal cash flows. Indeed, Asness (2003) shows that low-frequency movements in the U.S. inflation rate are almost entirely passed through to changes in the growth rate of nominal earnings for the S&P 500 index. Thus, to a first approximation, a real valuation number like the E/P ratio (or its inverse, the P/E ratio) should not move at all in response to changes in the nominal bond yield. Similar logic applies to the residential housing market; the ratio of house prices to rents (a real valuation number) should not be affected by inflation-induced changes in mortgage interest rates. Nevertheless, the data show that the ratio of house prices to rents in the U.S. economy has been trending up since the mid-1980s as inflation and mortgage interest rates have been trending down.
The observation that real valuation ratios are correlated with movements in nominal interest rates lends credence to the Modigliani-Cohn hypothesis. Investors and homebuyers appear to be adjusting their discount rates to match the prevailing nominal interest rate. However, for some unexplained reason, they do not simultaneously adjust their forecasts of future nominal cash flows, i.e., earnings distributions or imputed rents. The failure to take into account the influence of inflation on future nominal cash flows is an expectational error that is equivalent to discounting real cash flows using a nominal interest rate.
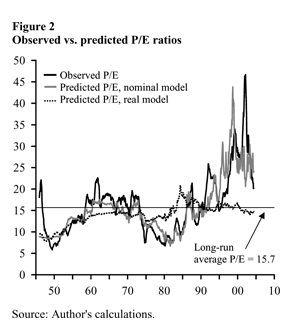 Asness (2000) shows that movements in the E/P ratio also appear to be driven by changes in investors’ risk perceptions. Monthly stock return volatility has declined relative to monthly bond return volatility, regardless of whether returns are measured in nominal or real terms. If investors’ risk perceptions are based on their own generation’s volatility experience, then stocks will appear to have become less risky relative to bonds over time. Following Asness, a statistical model of investor behavior can be constructed by regressing the E/P ratio on a constant term and three nominal explanatory variables: (1) the yield on a long-term government bond, (2) the volatility of monthly stock returns over the preceding 20 years, and (3) the volatility of monthly bond returns over the preceding 20 years. It turns out that this simple behavioral model can account for 70% of the variance in the observed E/P ratio from December 1945 to June 2004. In contrast, an otherwise identical model that employs real explanatory variables can account for only 26% of the variance in the observed E/P ratio. In Figure 2, the fitted E/P ratios from both the nominal and real models are inverted for comparison with the observed P/E ratio of the S&P 500 index. The nominal model does a much better job of matching the level and volatility of the observed P/E ratio. The real model, in contrast, predicts a relatively stable P/E ratio—one that remains close to its long-run average over much of the sample period, particularly during the so-called “new economy” years of the late 1990s and beyond. At the end of the sample period in June 2004, the observed P/E ratio is 20.2. The predicted P/E ratio from the nominal model is 24.1 while that from the real model is 14.8.
Asness (2000) shows that movements in the E/P ratio also appear to be driven by changes in investors’ risk perceptions. Monthly stock return volatility has declined relative to monthly bond return volatility, regardless of whether returns are measured in nominal or real terms. If investors’ risk perceptions are based on their own generation’s volatility experience, then stocks will appear to have become less risky relative to bonds over time. Following Asness, a statistical model of investor behavior can be constructed by regressing the E/P ratio on a constant term and three nominal explanatory variables: (1) the yield on a long-term government bond, (2) the volatility of monthly stock returns over the preceding 20 years, and (3) the volatility of monthly bond returns over the preceding 20 years. It turns out that this simple behavioral model can account for 70% of the variance in the observed E/P ratio from December 1945 to June 2004. In contrast, an otherwise identical model that employs real explanatory variables can account for only 26% of the variance in the observed E/P ratio. In Figure 2, the fitted E/P ratios from both the nominal and real models are inverted for comparison with the observed P/E ratio of the S&P 500 index. The nominal model does a much better job of matching the level and volatility of the observed P/E ratio. The real model, in contrast, predicts a relatively stable P/E ratio—one that remains close to its long-run average over much of the sample period, particularly during the so-called “new economy” years of the late 1990s and beyond. At the end of the sample period in June 2004, the observed P/E ratio is 20.2. The predicted P/E ratio from the nominal model is 24.1 while that from the real model is 14.8.
Inflation-induced valuation errors
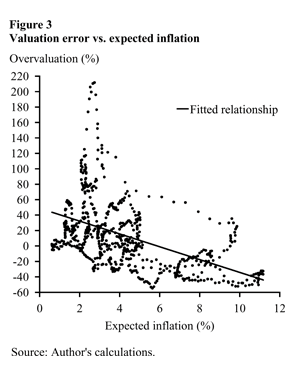 The predicted P/E ratio from the real model can be interpreted as an estimate of the rational (or fundamentals-based) P/E ratio because the model assumes that investors discount real cash flows using real interest rates. In this case, the difference between the observed P/E ratio and the real-model prediction can be viewed as a measure of overvaluation. Figure 3 shows that overvaluation (measured as a percent of fundamental value) is negatively correlated with the level of expected inflation; overvaluation tends to be high when expected inflation is low, and vice versa. According to the analysis, overvaluation was highest during the late 1990s and early 2000s—a period when expected and actual inflation were quite low. The late 1990s witnessed the emergence of the biggest bubble in history. The bubble burst in March 2000, setting off a chain of events that eventually dragged the U.S. economy into a recession in 2001. The recession-induced collapse in corporate earnings caused the market P/E ratio to spike above 45, thereby exceeding the previous high that had prevailed near the bubble peak. In contrast, the high inflation era of the late 1970s and early 1980s was characterized by substantial undervaluation, as the market P/E ratio languished below its long-run average for more than a decade. The results plotted in Figure 3 reinforce those of Ritter and Warr (2002) and Campbell and Vuolteenaho (2004), who find strong support for the Modigliani-Cohn hypothesis using more sophisticated empirical methods.
The predicted P/E ratio from the real model can be interpreted as an estimate of the rational (or fundamentals-based) P/E ratio because the model assumes that investors discount real cash flows using real interest rates. In this case, the difference between the observed P/E ratio and the real-model prediction can be viewed as a measure of overvaluation. Figure 3 shows that overvaluation (measured as a percent of fundamental value) is negatively correlated with the level of expected inflation; overvaluation tends to be high when expected inflation is low, and vice versa. According to the analysis, overvaluation was highest during the late 1990s and early 2000s—a period when expected and actual inflation were quite low. The late 1990s witnessed the emergence of the biggest bubble in history. The bubble burst in March 2000, setting off a chain of events that eventually dragged the U.S. economy into a recession in 2001. The recession-induced collapse in corporate earnings caused the market P/E ratio to spike above 45, thereby exceeding the previous high that had prevailed near the bubble peak. In contrast, the high inflation era of the late 1970s and early 1980s was characterized by substantial undervaluation, as the market P/E ratio languished below its long-run average for more than a decade. The results plotted in Figure 3 reinforce those of Ritter and Warr (2002) and Campbell and Vuolteenaho (2004), who find strong support for the Modigliani-Cohn hypothesis using more sophisticated empirical methods.
In recent years, contributors to the rapidly growing field of behavioral finance have been refining a new class of asset pricing models. These models are motivated by a variety of empirical and laboratory evidence which shows that people’s decisions and forecasts are often less than fully rational. Simple behavioral models can account for many observed features of real-world stock market data including: excess volatility of stock prices, time-varying volatility of returns, long-horizon predictability of returns, bubbles driven by optimism about the future, and market crashes that restore attention to fundamentals (see, for example, Lansing 2004 and the references cited therein).
Twenty-five years ago, Modigliani and Cohn (1979), put forth a behavioral model that predicted mispricing of stocks in the presence of changing inflation. The comovement of the stock market E/P ratio with the nominal bond yield observed since the mid-1960s (when U.S. inflation started rising) is consistent with the Modigliani-Cohn hypothesis. A regression model that includes a constant term and three nominal variables can account for 70% of the variance in the observed E/P ratio over the past four decades. However, as noted by Asness (2003), the success of this model in describing investor behavior should not be confused with the model’s ability to forecast what investors should really care about, namely, long-run real returns. Investors of the early 1980s probably did not anticipate the 20-year declining trend of inflation and nominal interest rates that helped produce above-average real returns as stocks moved from a state of undervaluation to one of overvaluation in the manner by described by Modigliani and Cohn (1979). Today’s investors may suffer the opposite fate if a secular trend of rising inflation and nominal interest rates causes the stock market to move back towards a state of undervaluation.
Kevin J. Lansing
Senior Economist
Asness, C.S. 2003. “Fight the Fed Model.” Journal of Portfolio Management 30(1) (Fall) pp. 11-24.
Asness, C.S. 2000. “Stocks versus Bonds: Explaining the Equity Risk Premium.” Financial Analysts Journal 56(2) pp. 96-113.
Campbell, J.Y., and T. Vuolteenaho. 2004. “Inflation Illusion and Stock Prices.” American Economic Review, Papers and Proceedings 94, pp. 19-23.
Hilsenrath, J.E. 2004. “Stock Characters: As Two Economists Debate Markets, the Tide Shifts.” Wall Street Journal, October 18, p. A1.
Lansing, K.J. 2004. “Lock-in of Extrapolative Expectations in an Asset Pricing Model.” FRBSF Working Paper 2004-06.
/economic-research/papers/2004/wp04-06bk.pdf
Modigliani, F., and R.A. Cohn. 1979. “Inflation, Rational Valuation and the Market.” Financial Analysts Journal 35, pp. 24-44.
Ritter, J.R., and R.S. Warr. 2002. “The Decline of Inflation and the Bull Market of 1982-1999.” Journal of Financial and Quantitative Analysis 37(1) pp. 29-61.
Stocks, Bonds, Bills, and Inflation 2004 Yearbook. 2004. Chicago: Ibbotson Associates.
Opinions expressed in FRBSF Economic Letter do not necessarily reflect the views of the management of the Federal Reserve Bank of San Francisco or of the Board of Governors of the Federal Reserve System. This publication is edited by Anita Todd and Karen Barnes. Permission to reprint portions of articles or whole articles must be obtained in writing. Please send editorial comments and requests for reprint permission to research.library@sf.frb.org