On September 20, the Federal Open Market Committee, the nation’s monetary policymaking body, raised its target level of the federal funds rate by 25 basis points, the eleventh straight increase over the last fifteen months. The statement released immediately after the meeting said, “With underlying inflation expected to be contained, the Committee believes that policy accommodation can be removed at a pace that is likely to be measured.
- Structural estimation of the neutral real interest rate
- Three problems with real-time estimation
- Conclusion
On September 20, the Federal Open Market Committee, the nation’s monetary policymaking body, raised its target level of the federal funds rate by 25 basis points, the eleventh straight increase over the last fifteen months. The statement released immediately after the meeting said, “With underlying inflation expected to be contained, the Committee believes that policy accommodation can be removed at a pace that is likely to be measured. Nonetheless, the Committee will respond to changes in economic prospects as needed to fulfill its obligation to maintain price stability.”
The statement clearly implies that the Committee believes that the real funds rate is below the so-called neutral real rate. What is the “neutral real rate”? According to Greenspan (1993), the real funds rate may be said to be neutral when it is at a level that, “if maintained, would keep the economy at its production potential over time.” Therefore, if the real funds rate is below the neutral real rate, policy is accommodative and the economy expands; if it is above the neutral real rate, policy is restrictive and the economy shrinks.
The difficulty policymakers face is that it is not obvious exactly what the level of the neutral real rate is. It cannot be observed directly. There is no reliable way to estimate it. And it can change.
This Economic Letter discusses the problems of estimation using both statistical methods and structural economic models. It focuses particularly on the vagaries of such estimations done in “real time,” that is, without the benefit of long and reliable series of data.
Structural estimation of the neutral real interest rate
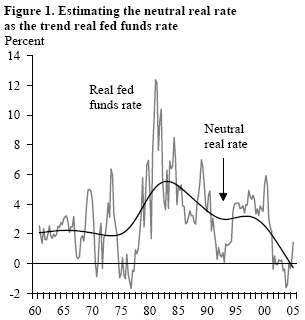 Because the neutral real interest rate is unobservable, economists have devised several strategies to estimate it. The simplest approach is to assume that it is equivalent to the trend real interest rate; this trend can be extracted from the real interest rate using statistical tools. For instance, the black line in Figure 1 plots one such measure by running what is known as a Hodrick-Prescott filter (in this figure, the real fed funds rate is defined using the deflator for personal consumption expenditures excluding food and energy). The estimated neutral real interest rate varies noticeably during the past four decades, from about 2% in the 1960s to almost 6% in the early 1980s and about 3% in the mid-1990s.
Because the neutral real interest rate is unobservable, economists have devised several strategies to estimate it. The simplest approach is to assume that it is equivalent to the trend real interest rate; this trend can be extracted from the real interest rate using statistical tools. For instance, the black line in Figure 1 plots one such measure by running what is known as a Hodrick-Prescott filter (in this figure, the real fed funds rate is defined using the deflator for personal consumption expenditures excluding food and energy). The estimated neutral real interest rate varies noticeably during the past four decades, from about 2% in the 1960s to almost 6% in the early 1980s and about 3% in the mid-1990s.
This simple statistical approach may be reasonable over periods when inflation and output growth are stable, but it leads to substantial biases when output or inflation varies significantly. For instance, inflation was rising during most of the 1970s, suggesting that the trend real interest rate was, in fact, well below its neutral level. Similarly, inflation fell rapidly in the early 1980s, suggesting that the average real interest rate was much higher than the neutral level. Thus the black line in Figure 1 underestimates the neutral real rate for the 1970s and overestimates it for the early 1980s.
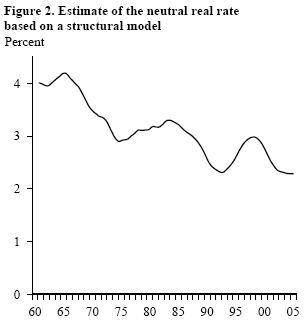 A more robust approach is to combine statistical tools with structural macroeconomic modeling techniques. Laubach and Williams (2003) provide a good example. There are three equations in their structural model: an “IS equation” relating the output gap (the deviation of actual output from its potential level) to the neutral real interest rate, a “Phillips curve” relating inflation to the output gap, and an equation describing the positive correlations between the neutral real rate and the trend growth of output, as predicted by economic theory. Once the macroeconomic model is specified, one can then estimate the neutral real interest rate through exploring the correlations between the interest rate, inflation, and output. For instance, when actual output exceeds trend output as predicted by the model, part of the unexpected strength in output will be attributed to a more accommodative monetary policy, which, in turn, implies that the neutral real interest rate was higher than otherwise projected.
A more robust approach is to combine statistical tools with structural macroeconomic modeling techniques. Laubach and Williams (2003) provide a good example. There are three equations in their structural model: an “IS equation” relating the output gap (the deviation of actual output from its potential level) to the neutral real interest rate, a “Phillips curve” relating inflation to the output gap, and an equation describing the positive correlations between the neutral real rate and the trend growth of output, as predicted by economic theory. Once the macroeconomic model is specified, one can then estimate the neutral real interest rate through exploring the correlations between the interest rate, inflation, and output. For instance, when actual output exceeds trend output as predicted by the model, part of the unexpected strength in output will be attributed to a more accommodative monetary policy, which, in turn, implies that the neutral real interest rate was higher than otherwise projected.
Figure 2 plots the estimate of the neutral real interest rate based on the Laubach-Williams model. The estimate suggests that, since the 1960s, the neutral real interest rate has fluctuated between 2% and 4%, and in early 2005 it stood around 2.25%. Note that for the 1970s, this estimate is significantly higher than the one based on the simple statistical approach, and for the 1980s, it is lower.
Translating the real neutral rate to the nominal neutral rate, given these estimates, would seem to be an easy exercise. For someone feeling comfortable with an inflation rate of 2%, for instance, the neutral federal funds rate would be around 4.25% at the moment. Unfortunately, it is not as easy as it seems.
Three problems with real-time estimation
Estimates of the neutral real interest rate based on the structural model can be quite imprecise. A recent study by Clark and Kozicki (2004) analyzes the difficulties in estimating today’s neutral real rate based on the contemporaneous data initially released historically (which would be called “real-time” estimates by economists), and concludes that such estimates “will be difficult to use reliably in practical policy applications” (p. 4). There are three major kinds of difficulties that arise, each of which can significantly bias the estimates.
The “one-sided filtering problem.” The first difficulty has to do with the so-called “one-sided filtering problem.” Statistical theory tells us that, in estimating unobservable variables, such as the neutral real interest rate, the more observations that are used in estimation, the more accurate the estimates will be. In reality, however, we can observe macroeconomic data only up to today. Therefore, the estimate of today’s neutral real rate based on data that are available today—called the “one-sided” estimate—will be quite different from the estimate when we have data beyond today—which are called the “two-sided” or “smoothed” estimates.
For instance, suppose we were back in 1990 and were trying to estimate the neutral real interest rate at that time. We would be able to perform the estimation based only on the data observed before 1990, since we would not know what inflation or real GDP growth is in 1991 or afterward. Now fast-forward to 2005. With the hindsight of an additional 15 years of data, we are able to revise our estimates based on a much longer sample, and our estimate of the neutral real interest rate for 1990 as of 2005 (the two-sided estimate) will be quite different from the one obtained in real time in 1990 (the one-sided estimate). Similarly, in estimating the neutral real interest rate in 2005, we are able to obtain only the one-sided estimate, which will be quite different from the two-sided estimate, which will take into account future data over the next decade or so.
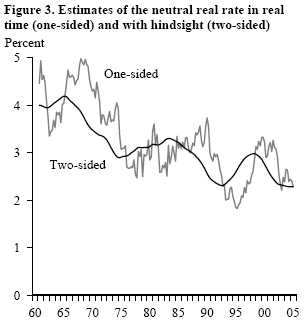 How much can the one-sided estimate differ from the more accurate two-sided estimate? The discrepancy could be as large as one to two percentage points, as Figure 3 shows. The gray line in the figure plots the one-sided estimates of the neutral real interest rate based on the data as observed in each quarter in the past 40 years, and the black line plots the two-sided estimates based on the data as observed to 2005. For instance, the one-sided estimate of the neutral real rate in 1990 is about 3.75%, whereas the two-sided estimate based on the data to 2005 is 2.5%.
How much can the one-sided estimate differ from the more accurate two-sided estimate? The discrepancy could be as large as one to two percentage points, as Figure 3 shows. The gray line in the figure plots the one-sided estimates of the neutral real interest rate based on the data as observed in each quarter in the past 40 years, and the black line plots the two-sided estimates based on the data as observed to 2005. For instance, the one-sided estimate of the neutral real rate in 1990 is about 3.75%, whereas the two-sided estimate based on the data to 2005 is 2.5%.
Data revisions. Another source of imprecision comes from the fact that macroeconomic data are often revised, and sometimes the revisions can be quite substantial. For instance, consider real GDP growth in the second quarter of 2001. According to the real-time macroeconomic data set collected by the Federal Reserve Bank of Philadelphia, it was initially estimated to be 0.7% at an annual rate; a few months later, it was revised down to 0.3%; a year later, it was revised down further to -1.6%; in mid-2003, it was revised up to -0.6%; as of 2005, it was finally revised up to 1.2%.
Such substantial revisions to the macroeconomic data will undoubtedly bias the estimates of both the model parameters and the neutral real interest rate. And the magnitude of the biases will depend on the size of the data revisions. Clark and Kozicki (2004) investigate this problem using 40 years of real-time data for the U.S. and find that such biases could be as high as one to two percentage points.
Uncertainties about model specification. Our discussion so far assumes that the macroeconomic model underlying the estimates of the neutral rate is the correct one. However, there are alternative ways to model the economy, and macroeconomists have not reached a consensus about which one is most reliable.
Different model specifications can generate very different estimates of the neutral real interest rate. Indeed, Clark and Kozicki (2004) find that estimates of the neutral real interest rate are sensitive to model specification and that these differences can again be as large as one to two percentage points. Therefore, given all three kinds of uncertainties, it would not be surprising to have a total bias of two percentage points or more in estimating the neutral real interest rate.
Economists have highlighted numerous difficulties in estimating the neutral federal funds rate in real time, including data and model uncertainty, which can result in estimates that are off by a couple of percentage points. These difficulties add to the challenge of conducting monetary policy, especially when the federal funds target is near the neutral rate, because policymakers must make their decisions without the benefit of reliable data. Therefore, policymakers will be especially attentive at this stage to incoming data. And, until research finds a solution to the difficulties of estimating the neutral rate, the conduct of policy will remain both a science and an art.
Tao Wu
Economist
References
[URLs accessed October 2005.]
Clark, Todd, and Sharon Kozicki. 2004. “Estimating Equilibrium Real Interest Rates in Real Time.” FRB Kansas City Working Paper 2004-08. http://www.kc.frb.org/publicat/reswkpap/pdf/rwp04-08.pdf
Greenspan, Alan, 1993. Testimony on 1993 Monetary Policy Objectives to the U.S. Senate, July 20.
Laubach, Thomas, and John Williams. 2003. “Measuring the Natural Rate of Interest.” The Review of Economics and Statistics 85(4) (November) pp. 1063-1070.
Opinions expressed in FRBSF Economic Letter do not necessarily reflect the views of the management of the Federal Reserve Bank of San Francisco or of the Board of Governors of the Federal Reserve System. This publication is edited by Anita Todd and Karen Barnes. Permission to reprint portions of articles or whole articles must be obtained in writing. Please send editorial comments and requests for reprint permission to research.library@sf.frb.org