From January 2000 through this past June, the 10-year U.S. Treasury bond yield has moved over a wide range, falling from 6.8% in early 2000 to 3.1% in June 2003 and rising back to over 5% more recently. The interest rate on 30-year fixed-rate mortgages has similarly varied from a high of 8.6% in 2000 to a low of 5.2% in June 2003 and back to about 6.75% more recently.
- What is the term premium?
- Measuring the term premium
- Limitations to our understanding of the term premium
- Summary and conclusions
- References
From January 2000 through this past June, the 10-year U.S. Treasury bond yield has moved over a wide range, falling from 6.8% in early 2000 to 3.1% in June 2003 and rising back to over 5% more recently. The interest rate on 30-year fixed-rate mortgages has similarly varied from a high of 8.6% in 2000 to a low of 5.2% in June 2003 and back to about 6.75% more recently. These fluctuations translate into huge variation in the debt financing costs of the U.S. government and in the prospective monthly mortgage payments of U.S. homebuyers.
What caused these large fluctuations? In July 2005, Alan Greenspan, then Chairman of the Federal Reserve Board, reported to Congress that “a significant portion of the sharp decline in [long-term interest rates] over the past year appears to have resulted from a fall in term premiums” (Greenspan 2005). While this is not the only possible explanation for movements in long-term interest rates, the term premium is nonetheless an important component of these rates. Thus, understanding long-term interest rate fluctuations requires one to understand what the term premium is and how it may change over time.
In this Economic Letter, we define the term premium and explain the state of the art in measuring it. Unfortunately, the term premium turns out to be very difficult to measure; thus, we conclude with some discussion of the limitations of our current knowledge.
Briefly stated, the term premium is the excess yield that investors require to commit to holding a long-term bond instead of a series of shorter-term bonds. For example, suppose that the interest rate on the 10-year U.S. Treasury note is about 5.5%, and suppose that the interest rate on the 1-year U.S. Treasury bill is expected to average about 5% over the next 10 years (“note” and “bill” are the customary names for U.S. Treasury securities of these maturities). Then the term premium on the 10-year U.S. Treasury note would be about 0.5%, or 50 basis points.
Thus, a key component of the term premium is investor expectations about the future course of short-term interest rates over the lifetime of the long-term bond. In the example above, the term premium on the 10-year Treasury note depends crucially on financial market expectations about the course of shorter-term U.S. interest rates over the next ten years, a very long horizon. This foreshadows some of the difficulties of measuring the term premium that we will encounter below.
Note that, while we usually think of the term premium as being positive–that financial market participants require extra yield to induce them to hold a bond for a longer period of time–there is nothing in the definition of the term premium that requires it to be so. For example, if some purchasers of long-term debt, such as pension funds, are interested in locking in a fixed rate of return for a long period of time, they could be willing to accept a lower yield on long-term securities (a negative term premium) in order to avoid the risks associated with rolling over their investments in a series of shorter-term bonds with uncertain, fluctuating interest rates. Thus, both the sign and the magnitude of the term premium are ultimately empirical questions.
In principle, it is easy to measure the term premium using the definition in the previous section, but this requires us to obtain data on or to estimate financial markets’ expectations about the future course of short-term interest rates over a fairly long horizon. There are many possible ways one might go about doing this, of which we now highlight four:
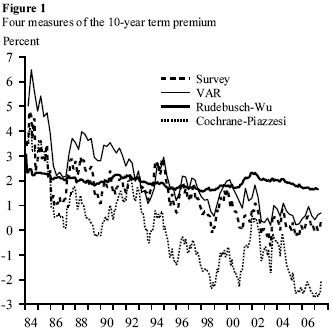1. Survey-based measure. One can simply survey financial market participants regarding their expectations for future short-term interest rates and plug those forecasts into the definition of the term premium above. Unfortunately, surveys of market participants about their interest rate forecasts over such long horizons are conducted very infrequently and may suffer from substantial rounding error (since respondents report only very rough average estimates of future rates) and other problems. In Figure 1, we make use of what long-term survey data there are and plot a survey-based measure of the term premium as the dashed line. The data on market expectations come from the Blue Chip Survey of forecasters, which asks respondents for their long-horizon forecasts of the 3-month Treasury bill rate twice per year, every March and September. We interpolate between these semiannual survey forecasts to create the monthly frequency plot in Figure 1.
2. VAR-based measure. Because long-term survey data are available so infrequently and because survey responses are sometimes not very good measures of financial markets’ true expectations as embodied in market prices, it may make sense to use a macroeconomic forecasting model such as a vector autoregression (VAR) to forecast short-term interest rates instead. Plugging these VAR-based forecasts into the definition of the term premium then provides an alternative and more timely measure, which we depict by the solid thin line in Figure 1.
3. RW model-based measure. Instead of a VAR, one can forecast interest rates using a New Keynesian macroeconomic model. For example, the RW (Rudebusch and Wu 2003) model has some advantages over a VAR for forecasting long-term interest rates, such as allowing the market’s long-run expected rate of inflation in the economy to vary over time, which is likely to have been a very important factor in the 1980s and which some studies (for example, Gürkaynak, Sack, and Swanson 2005) have found to be important for explaining movements in U.S. long-term bond yields even in recent years. (The RW model also satisfies the “arbitrage-free” conditions mentioned below, which ensure that the yield curve at any point in time is consistent with its future evolution over time.) We plot this RW model-based measure of the term premium as the solid thick line in Figure 1.
4. Cochrane-Piazzesi measure. In contrast to survey-based or model-based approaches to measuring expectations and the term premium, Cochrane and Piazzesi (2005) developed a purely empirical measure of the expected excess total return (yield plus capital gain) on long-term Treasury securities over the next year. These expected one-year excess total returns, together with the current one-year interest rate, can be iterated forward to compute the expected excess return for each of the next ten years, thereby producing a measure of the 10-year term premium, which we plot as the dotted line in Figure 1.
The measures above represent just four out of many possible approaches to measuring market expectations and the term premium. For example, Cochrane (2007) considers two different specifications of a VAR and shows that the resulting term premium estimates are vastly different, even though both measures are derived from a VAR and thus might be expected to be similar. Rudebusch, Sack, and Swanson (2007) also compare several of the above measures to “arbitrage-free” term premium estimates that are standard in the finance literature, such as the Kim-Wright (2005) measure that is produced by Federal Reserve Board staff and frequently cited in speeches and testimony by Federal Reserve Board officials.
Limitations to our understanding of the term premium
Despite displaying some basic similarities, the four measures of the term premium depicted in Figure 1 are strikingly different. First, three of the four measures show large secular declines over time, while one measure (the one from the Rudebusch-Wu model) shows a much smaller decrease; that is, the RW model attributes almost all of the decline in long-term interest rates over the past 20 years to a fall in market expectations for inflation and the future path of short-term interest rates rather than to a fall in the term premium.
Second, in June 2007, the most recent month in the figure, the four estimates of the term premium range from -2% up to 2%–a tremendous difference considering that the 10-year Treasury yield has been only about 5%. Even the Survey and VAR measures, which have tracked each other fairly closely since 1993, differ by about 50 basis points. Thus, we cannot even say with much certainty whether the term premium is positive or negative at present.
Third, the Survey, VAR, and Cochrane-Piazzesi measures of the term premium all show substantial short-term fluctuations, while the Rudebusch-Wu measure is much smoother over time. That is, the RW model is much more likely to attribute fluctuations in long-term bond yields to changes in market expectations about long-run inflation and the future path of short-term interest rates, while the other three measures are much more likely to attribute these movements in long-term bond yields to changes in the term premium.
Why are these measures of the term premium so different? The answer is that any estimate of the term premium depends crucially on the markets’ expectations of the future path of short-term interest rates for the next ten years, and these expectations are very difficult to measure for such long horizons. Our uncertainty regarding the markets’ expectations of inflation and short-term interest rates in the far-distant future is reflected in our uncertainty regarding the current level of the term premium.
Long-term interest rates have moved a great deal in recent years as well as over the past few decades. A key component of long-term interest rates is the term premium, and many financial market analysts have attributed a substantial fraction of the changes in long-term interest rates to changes in the term premium. While this may be true, there are daunting limitations in our ability to measure the term premium, so it is very difficult to make any such claims with confidence. In the future, better surveys and research into better econometric techniques will hopefully improve the accuracy of our measurements of the term premium and improve our understanding of this important component of long-term interest rates.
Eric Swanson
Research Advisor
[URLs accessed July 2007.]
Cochrane, John. 2007. “Commentary on ‘Macroeconomic Implications of Changes in the Term Premium.’” FRB St. Louis Review 89(4) (July/August) pp. 271-282. http://research.stlouisfed.org/publications/review/07/07/Cochrane.pdf
Cochrane, John, and Monika Piazzesi. 2005. “Bond Risk Premia.” American Economic Review 95(1) (March) pp. 138-160.
Greenspan, Alan. 2005. “Federal Reserve Board’s Semiannual Monetary Policy Report to Congress,” July 20. http://www.federalreserve.gov/boarddocs/hh/2005/july/testimony.htm
Gürkaynak, Refet, Brian Sack, and Eric Swanson. 2005. “The Sensitivity of Long-Term Interest Rates to Economic News: Evidence and Implications for Macroeconomic Models.” American Economic Review 95(1) (March) pp. 425-436.
Kim, Don, and Jonathan Wright. 2005. “An Arbitrage-Free Three-Factor Term Structure Model and the Recent Behavior of Long-Term Yields and Distant-Horizon Forward Rates.” Federal Reserve Board Finance and Economics Discussion Series 2005-33. http://www.federalreserve.gov/pubs/feds/2005/200533/200533abs.html
Rudebusch, Glenn, Brian Sack, and Eric Swanson. 2007. “Macroeconomic Implications of Changes in the Term Premium.” FRB St. Louis Review 89(4) (July/August) pp. 241-269. http://research.stlouisfed.org/publications/review/07/07/Rudebusch.pdf
Rudebusch, Glenn, and Tao Wu. 2003. “A Macro-Finance Model of the Term Structure, Monetary Policy, and the Economy.” FRB San Francisco Working Paper 2003-17, forthcoming in The Economic Journal. /economic-research/papers/2003/wp03-17bk.pdf
Opinions expressed in FRBSF Economic Letter do not necessarily reflect the views of the management of the Federal Reserve Bank of San Francisco or of the Board of Governors of the Federal Reserve System. This publication is edited by Anita Todd and Karen Barnes. Permission to reprint portions of articles or whole articles must be obtained in writing. Please send editorial comments and requests for reprint permission to research.library@sf.frb.org