Speculative bubbles have occurred throughout history in numerous countries and asset markets. The term “bubble” was coined in England in 1720 following the famous price run-up and crash of shares in the South Sea Company.
- Bubbles and excess volatility
- Irrational exuberance versus rational speculation
- Near-rational bubbles
- Conclusion
- References
Nowhere does history indulge in repetitions so often or so uniformly as in Wall Street. When you read contemporary accounts of booms or panics the one thing that strikes you most forcibly is how little either stock speculation or stock speculators today differ from yesterday. The game does not change and neither does human nature.
–From the thinly disguised biography of legendary speculator Jesse Livermore, by E. Lefèvre (1923, p. 180).
Speculative bubbles have occurred throughout history in numerous countries and asset markets. The term “bubble” was coined in England in 1720 following the famous price run-up and crash of shares in the South Sea Company. The run-up led to widespread public enthusiasm for the stock market and a proliferation of highly suspect companies attempting to sell shares to investors. One such venture notoriously advertised itself as “a company for carrying out an undertaking of great advantage, but nobody to know what it is.” The epidemic of fraudulent stock-offering schemes led the British government to pass the so-called “Bubble Act” in 1720, which was officially named “An Act to Restrain the Extravagant and Unwarrantable Practice of Raising Money by Voluntary Subscription for Carrying on Projects Dangerous to the Trade and Subjects of the United Kingdom.” Throughout history, speculative bubbles have usually coincided with outbreaks of fraud and scandal, followed by calls for more regulation once the bubble has burst (see Gerding 2006).
Economists use the term “bubble” to describe an asset price that has risen above the level justified by economic fundamentals, as measured by the discounted stream of expected future cash flows that will accrue to the owner of the asset. The dramatic rise in U.S. stock prices during the late 1990s, followed similarly by U.S. house prices during the early 2000s, are episodes that have both been described as “bubbles.” This Economic Letter describes some research that attempts to account for the behavior of asset price bubbles.
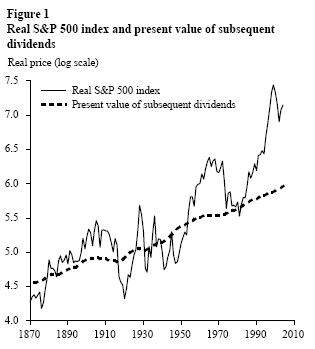 Numerous empirical studies, starting with Shiller (1981) and LeRoy and Porter (1981), have demonstrated that stock prices appear to exhibit “excess volatility.” To illustrate the basic idea, Figure 1 plots the real (inflation-adjusted) value of the S&P 500 stock index from 1871 to 2004, together with the present value of subsequent real dividends, where dividends beyond 2004 are presumed to grow at the historical average rate. The constant discount rate used in the present value calculation is the geometric-average real return on stocks over the full sample–a measure of rational investors’ required rate of return. The use of a variable discount rate does not change the basic conclusions, as shown by Shiller (2003).
Numerous empirical studies, starting with Shiller (1981) and LeRoy and Porter (1981), have demonstrated that stock prices appear to exhibit “excess volatility.” To illustrate the basic idea, Figure 1 plots the real (inflation-adjusted) value of the S&P 500 stock index from 1871 to 2004, together with the present value of subsequent real dividends, where dividends beyond 2004 are presumed to grow at the historical average rate. The constant discount rate used in the present value calculation is the geometric-average real return on stocks over the full sample–a measure of rational investors’ required rate of return. The use of a variable discount rate does not change the basic conclusions, as shown by Shiller (2003).
Theory says that the observed price of a stock represents the rational forecast of the discounted stream of future dividends that will be paid to shareholders. One characteristic of a rational forecast is that it should be less variable than the object being forecasted. This principle appears to be grossly violated in the case of stock prices. Figure 1 shows that the observed stock price (the forecast) appears to be much more variable than the present value of subsequent dividends (the object being forecasted). Bubble models may help account for this excess volatility because they allow stock prices to become detached from fundamentals.
Irrational exuberance versus rational speculation
Shiller (2005) describes a simple and intuitive feedback model of bubbles. If asset prices start to rise, the success of some investors attracts public attention that fuels the spread of enthusiasm for the market. New (often less sophisticated) investors enter the market and bid up prices. This “irrational exuberance” heightens expectations of further price increases, as investors extrapolate recent price action far into the future. The market’s meteoric rise is typically justified in the popular culture by some superficially plausible “new era” theory that validates the abandonment of traditional valuation metrics. But the bubble carries the seeds of its own destruction; if prices begin to sag, pessimism can take hold, causing some investors to exit the market. Downward price motion begets expectations of further downward motion, and so on, until a bottom is eventually reached.
Shiller’s feedback model says that investors eschew fundamentals in favor of simple price extrapolation rules. Along these lines, Lansing (2006) shows how an individual investor may become “locked in” to the use of an extrapolative forecast rule if other investors are following the same approach. From the perspective of an individual investor, switching to a fundamentals-based forecast would appear to reduce forecast accuracy, so there is no incentive to do so. The term “lock-in” borrows from research on the choice among competing technologies. The original contributions of David (1985) and Arthur (1989) argue that early chance events or “historical accidents” may cause people to initially choose, and then stick with, an inferior technology. In the case of stocks, extrapolative forecast rules can be viewed as an inferior technology because market predictions would improve if all investors could be induced to switch to a fundamentals-based approach.
In contrast to Shiller’s irrational exuberance view, so-called “rational bubble” models say that investors are fully cognizant of an asset’s fundamental value, but nevertheless they may be willing to pay more than this amount. This can occur if expectations of future price appreciation are large enough to satisfy the rational investor’s required rate of return. To sustain a rational bubble, the stock price must grow faster than dividends (or cash flows) in perpetuity.
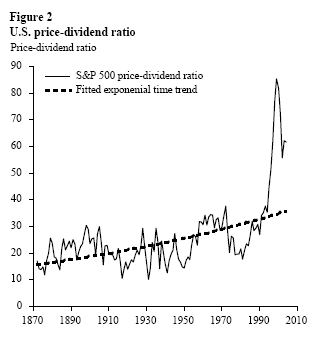 Figure 2 plots the U.S. price-dividend ratio from 1871 to 2004 together with an estimated exponential time trend. The estimated trend is around 1 percent per year. If this trend were to continue indefinitely, as implied by a rational bubble model, then the U.S. price-dividend ratio would double about every 72 years–a seemingly unrealistic model of long-run market behavior. Indeed, Hall (2001, p. 3) dismisses the idea that “intelligent people [would] believe that the value of a stock will become larger and larger in relation to all other quantities in the economy.” Froot and Obstfeld (1991, p. 1190) acknowledge that “It is difficult to believe that the market is literally stuck for all time on a path along which price-dividend ratios eventually explode.” A more elaborate model assumes that the bubble will periodically crash according to some universally known probability function, but this is an ad hoc feature that is determined completely outside of the model.
Figure 2 plots the U.S. price-dividend ratio from 1871 to 2004 together with an estimated exponential time trend. The estimated trend is around 1 percent per year. If this trend were to continue indefinitely, as implied by a rational bubble model, then the U.S. price-dividend ratio would double about every 72 years–a seemingly unrealistic model of long-run market behavior. Indeed, Hall (2001, p. 3) dismisses the idea that “intelligent people [would] believe that the value of a stock will become larger and larger in relation to all other quantities in the economy.” Froot and Obstfeld (1991, p. 1190) acknowledge that “It is difficult to believe that the market is literally stuck for all time on a path along which price-dividend ratios eventually explode.” A more elaborate model assumes that the bubble will periodically crash according to some universally known probability function, but this is an ad hoc feature that is determined completely outside of the model.
From a theoretical perspective, rational bubbles must always be positive, i.e., the stock price must always exceed its fundamental value. By definition, rational expectations must be correct on average. So, if rational investors expected the stock price to depreciate below its fundamental value, then they would be unwilling to overpay for the stock in the first place, i.e., the bubble would never get started. Also, there must be an infinite number of market participants. Otherwise, the market would eventually run out of rational investors who are willing to overpay now for an asset in order to sell later (at a higher price) to another rational investor. While some have argued that theoretical conditions like these rule out the existence of rational bubbles, others disagree. LeRoy (2004, p. 801) remarks, “It is a testament to economists’ capacity for abstraction that they have accepted without question that an intricate theoretical argument against [rational] bubbles has somehow migrated from the pages of Econometrica [a top academic journal] to the floor of the New York Stock Exchange.”
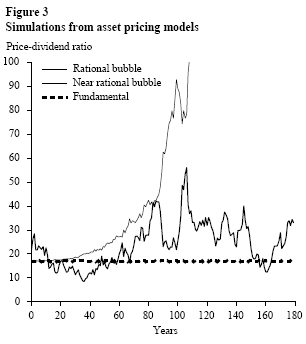 Rational bubble models assume that investors always know the size of the bubble–to the point of constructing separate forecasts for the fundamental and bubble components of the stock price. Real world investors may be inclined to construct only a single forecast that attempts to predict the movement of the total stock price (fundamental plus bubble). Adopting this setup, Lansing (2007) develops a “near-rational” bubble model in which investors fit a simple extrapolative forecast rule to observable stock market data. The resulting price-dividend ratio exhibits pronounced upward and downward swings, giving rise to excess volatility, but the ratio always returns to the vicinity of a long-run average, unlike a rational bubble. Also unlike its rational counterpart, the near-rational bubble can occasionally become negative, causing the stock price to dip below its fundamental value.
Rational bubble models assume that investors always know the size of the bubble–to the point of constructing separate forecasts for the fundamental and bubble components of the stock price. Real world investors may be inclined to construct only a single forecast that attempts to predict the movement of the total stock price (fundamental plus bubble). Adopting this setup, Lansing (2007) develops a “near-rational” bubble model in which investors fit a simple extrapolative forecast rule to observable stock market data. The resulting price-dividend ratio exhibits pronounced upward and downward swings, giving rise to excess volatility, but the ratio always returns to the vicinity of a long-run average, unlike a rational bubble. Also unlike its rational counterpart, the near-rational bubble can occasionally become negative, causing the stock price to dip below its fundamental value.
Figure 3 plots simulations of the price-dividend ratio for the rational and near-rational bubble models, together with the results of a purely fundamentals-based model. Empirical studies find evidence that U.S. stock prices drift upwards into bubble territory during bull markets, but these persistent departures from fundamentals are eventually eliminated via downward adjustments during bear markets. The near-rational model captures these and other features of the data, as detailed further in Lansing (2007).
Theories involving departures from rational behavior have long played a role in efforts to account for movements in stock prices. Keynes (1936, p. 156) likened the stock market to a “beauty contest” where participants devoted their efforts not to judging the underlying concept of beauty, but instead to “anticipating what average opinion expects the average opinion to be.” Keynes readily acknowledged the concept of irrational, herd-like behavior among investors in stating: “There is no clear evidence from experience that the investment policy which is socially advantageous coincides with that which is most profitable” (p. 157). He cautioned that it may be “scarcely practicable” to employ a rational, long-term investment strategy in a market dominated by short-term “game-players.” More recently, Federal Reserve Chairman Alan Greenspan (1999) warned that “an unwarranted, perhaps euphoric, extension of recent developments can drive equity prices to levels that are unsupportable…. Such straying above fundamentals could create problems for our economy when the inevitable adjustment occurs.” Incorporating the flavor of these ideas into quantitative economic models is a promising area of ongoing research.
Kevin J. Lansing
Senior Economist
Arthur, W.B. 1989. “Competing Technologies, Increasing Returns, and Lock-in by Historical Small Events.” Economic Journal 99, pp. 116-131.
David, P. 1985. “Clio and the Economics of QWERTY.” American Economic Review, Papers and Proceedings 75, pp. 332-337.
Froot, K., and M. Obstfeld. 1991. “Intrinsic Bubbles: The Case of Stock Prices.” American Economic Review 81, pp. 1189-1214.
Gerding, E.F. 2006. “The Next Epidemic: Bubbles and the Growth and Decay of Securities Regulation.” Connecticut Law Review 38(3), pp. 393-453.
Greenspan, A. 1999. “The Federal Reserve’s Semiannual Report on Monetary Policy.” Testimony before the Committee on Banking and Financial Services, U.S. House of Representatives, July 22.
Hall, R.E. 2001. “Struggling to Understand the Stock Market.” American Economic Review Papers and Proceedings 91, pp. 1-11.
Keynes, J.M. 1936. The General Theory of Employment, Interest, and Money.” New York: Harcourt-Brace.
Lansing, K.J. 2006. “Lock-in of Extrapolative Expectations in an Asset Pricing Model.” Macroeconomic Dynamics 10, pp. 317-348.
Lansing, K.J. 2007. “Rational and Near Rational Bubbles without Drift.” FRBSF Working Paper 2007-10.
Lefèvre, E. 1923. Reminiscences of a Stock Operator. New York: John Wiley (originally published by G.H. Doran).
LeRoy, S.F. 2004. “Rational Exuberance.” Journal of Economic Literature 152, pp. 783-804.
LeRoy, S.F., and R.D. Porter. 1981. “The Present-Value Relation: Tests Based on Implied Variance Bounds.” Econometrica 49, pp. 555-577.
Shiller, R.J. 1981. “Do Stock Prices Move Too Much to Be Justified by Subsequent Changes in Dividends?” American Economic Review 71, pp. 421-436.
Shiller, R.J. 2003. “From Efficient Markets Theory to Behavioral Finance.” Journal of Economic Perspectives 17 (Winter), pp. 83-104.
Shiller, R.J. 2005. Irrational Exuberance, Second Edition. Princeton, NJ: Princeton University Press.
Opinions expressed in FRBSF Economic Letter do not necessarily reflect the views of the management of the Federal Reserve Bank of San Francisco or of the Board of Governors of the Federal Reserve System. This publication is edited by Anita Todd and Karen Barnes. Permission to reprint portions of articles or whole articles must be obtained in writing. Please send editorial comments and requests for reprint permission to research.library@sf.frb.org