A major advancement in risk management among large financial institutions has been the development of internal risk models. The models encompass institutions’ procedures and techniques for assessing portfolio risk.
A major advancement in risk management among large financial institutions has been the development of internal risk models. The models encompass institutions’ procedures and techniques for assessing portfolio risk. Commercial bank regulators in the U.S. and abroad have recognized that these “state of the art” risk-management tools provided a framework for addressing important shortfalls of current capital regulations. To that end, a key component of the new rules for bank capital regulation developed under the Basel II agreement allows for banks’ internal risk-management systems to be part of the regulatory framework. This is known as the advanced approach and is intended for the largest and most sophisticated banking organizations.
Key elements of internal risk models used under the advanced approach are the estimated probabilities of default (PDs) for bank assets. For example, a bank using the advanced approach would be required to deliver an estimate of the one-year PD for each corporate exposure. This Economic Letter describes some of the problems involved in estimating the required one-year PDs from banks’ internal ratings data and details the approach taken in Christensen, Hansen, and Lando (2004) to address them.
As part of the Basel II advanced approach, banking organizations would have a range of risk categories, or “risk buckets,” and at least once a year they would have to monitor and evaluate the credit quality of each borrower. For corporate exposures, for example, each bucket has an estimated PD associated with the assets in the given bucket. These risk buckets are similar in concept to the different risk ratings for corporate debt used by rating agencies, such as Moody’s, Standard & Poor’s, and Fitch.
For banking organizations, the number of buckets and the process for deriving the default probabilities are part of their internal risk models and will vary among institutions. Current practices for estimating the probability of, say, loans to a corporation in a given risk category “transitioning” to the default category are dominated by the so-called cohort approach. This approach is a discrete-time model; that is, the firms in a given rating category are tracked over a fixed period, such as a year. The estimated probability of a transition to default is simply the ratio of the observed number of firms that made that transition to default, say, over one-year intervals, to the number of firms that started in the rating category at the beginning of each year considered.
As part of their risk-management systems, banks are also interested in the transition probabilities of assets to risk categories other than default. Accordingly, the cohort approach is commonly used to estimate how likely it is for an asset in, say, a medium risk category to transition to lower or to higher risk categories. In risk-management parlance, the entire set of such possible changes in ratings is referred to as a transition matrix.
One drawback of the cohort approach for determining PDs using an interval such as one year is that we obtain an estimate of zero probability if no such transition has occurred; one typical example of this would be the transition to default by a very highly rated firm. However, while the probability that a firm rated Aaa transitioning to default in a given year is certainly low, it is doubtful that the true probability is exactly zero. For banking organizations at least, Basel II’s advanced approach attempts to address this drawback by requiring the imposition of a minimum probability of 0.03%.
There are two other drawbacks associated with the discrete-time cohort approach to estimating transition probability matrices. One is that using a fixed time horizon for estimating transitions limits the flexibility to consider intermediate or longer time horizons. The other is that the approach typically does not distinguish between firms with stable ratings and firms that have recently had their ratings changed. This distinction can matter. As Fledelius, Lando, and Nielsen (2004) show in examining the dynamic pattern of rating changes, a firm that was recently upgraded (downgraded) is initially at an increased risk of being further upgraded (downgraded) compared to firms that have had the same corresponding rating for an extended period. They find that this effect disappears on average after 24 to 30 months. One explanation for the increased risk of further regrading is that the agencies may prefer to adjust ratings very gradually rather than in one fell swoop; for example, if a rating agency believes that a firm needs to be downgraded several notches, it may proceed one notch at a time to ensure that, as time passes and events unfold, the rating change is warranted.
In Christensen, Hansen, and Lando (2004), we present a model which attempts to improve on all three limitations of the standard cohort approach. The theoretical model is formulated in continuous time, which has two immediate advantages. The first advantage is that it delivers nonzero estimates for all transition probabilities. The second advantage is that we can estimate transition probabilities for any time horizon, not just for the one-year horizon. Third, the model allows for transition probabilities to vary for similarly rated assets with recent rating changes and those with stable (longer-standing) ratings.
In applying the model, we use ratings data from Moody’s. To make estimation manageable, we reduce the number of ratings in the usual way: Aa1, Aa2, and Aa3 are merged into a single Aa rating. Proceeding in a similar way for the other rating categories we end up with a system of eight ratings (Aaa, Aa, A, Baa, Ba, B, Caa, D), where D denotes the default state. The distinction between stable-rated firms and firms that have recently had their ratings changed is taken into consideration by extending the number of ratings to include four additional so-called excited states (Ba*, B*, Caa*). The idea behind this extension is that firms are downgraded to the excited state of that rating category where they stay until they are either upgraded or further downgraded, or until they make the unobserved transition from the excited state to the comparable normal rating–for example, Baa* to Baa. Since we are primarily interested in measuring the risk of drifting through the ratings towards the default state, this analysis does not include excited states for upgrades.
As an approximation to continuous time, we use daily data in estimating our model. To control for differences in market conditions, we estimate the model over two separate five-year periods. The first period covers the volatile years from 1987 to 1991 containing a deep recession and the savings and loan crisis. The second is the much calmer period from 1995 to 1999 characterized by a generally benign economic environment.
The key point to note is that the statistical power of our model is derived primarily from the rating transitions of non-defaulting firms. For example, we do not actually have to observe transitions from the Aaa rating to default to estimate the probability of such a transition. From the daily data we have some transitions from the Aaa rating to the A rating, from A ratings to other lower ratings, and from the lower ratings to default. The model in effect links the information on the array of transitions to estimate the likelihood of the very low probability events. In contrast, the standard cohort approach does not make a connection between the ratings transitions of surviving firms and those of firms that default.
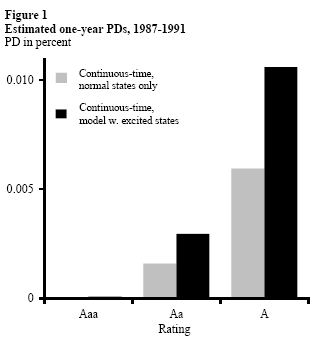In this section we highlight two of the advantages of our model–obtaining estimates for very low probability events and incorporating the effects from making the distinction between securities of stable firms and those of firms that have recently been downgraded. In doing so, we discuss two estimates of one-year PDs for each rating category. The estimates using the daily observations with just the eight standard rating categories (also denoted “normal states only”) are the standard estimates. The estimates that also include the four excited states are the excited estimates. The estimates shown in the figures are for the more volatile period, 1987 to 1991.
Figure 1 shows the estimated transition probabilities for the higher-rated firms. Under the simple cohort approach, the one-year PD is zero for the three top ratings. The standard and the excited estimates of the one-year probabilities are quite low, but not zero. For the A-rated category, the highest point estimate (the excited estimate) is 0.0106%. Our model estimates therefore suggest that the Basel II requirement of assigning at least a 0.03% default transition probability is conservative. For example, for the A-rated category the top of the 95% confidence interval from our model is 0.02% for the 1987 to 1991 period (and only 0.001% in the 1995 to 1999 period).
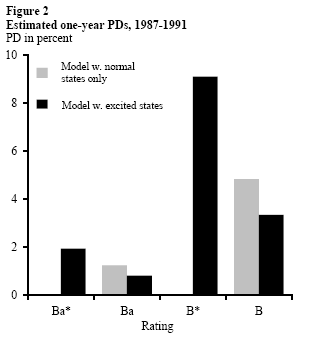The results from our model also show that introducing a distinction between stable firms and firms that have recently been downgraded is supported by the data. For the top rated firms in Figure 1, the inclusion of the excited states doubles the estimated one-year PDs of these three categories in the volatile period from 1987 to 1991 (and increases them by a factor of 8 in the calm period from 1995 to 1999). For the remaining non-default categories, where there are both excited and stable categories, the general pattern is that the one-year PD estimates are higher for the excited states and lower for the stable states than the estimates obtained for the corresponding ratings in the model without excited states. Figure 2 illustrates this for the (Ba*, Ba, B*, B) categories over the 1987 to 1991 period.
This Economic Letter describes one approach to addressing some of the obstacles banks face in estimating one-year PDs for use in internal risk models. Applying those methods to ratings data from Moody’s, we find that the one-year PDs can be reliably estimated from a data set of that quality. Also, we find that distinguishing between stable and recently downgraded firms in the model increases the estimated PDs notably for highly rated firms and recently downgraded firms, while lowering the estimated PDs for firms with stable ratings. Regarding the implication of the model in the context of Basel II for a given bank, the required amount of capital could go up or down. In particular, the results indicate that incorporating the distinction between recently re-rated firms and firms with stable ratings into the estimation does not make the estimated one-year PDs for the three top ratings go beyond the imposed minimum of 0.03%. Thus, the capital requirements applicable to the top rated corporate exposures would not be affected. For the remaining categories, the distinction may alleviate the capital requirement if a bank’s portfolio contains sufficiently many stable firms relative to the number of recently downgraded firms.
Jens Christensen
Economist
Christensen, Jens, Ernst Hansen, and David Lando. 2004. “Confidence Sets for Continuous-Time Rating Transition Probabilities.” Journal of Banking and Finance 28, pp. 2,575-2,602.
Fledelius, Peter, David Lando, and Jens Perch Nielsen. 2004. “Non-Parametric Analysis of Rating Transition and Default Data.” Journal of Investment Management 2(2), pp. 71-85.
Opinions expressed in FRBSF Economic Letter do not necessarily reflect the views of the management of the Federal Reserve Bank of San Francisco or of the Board of Governors of the Federal Reserve System. This publication is edited by Anita Todd and Karen Barnes. Permission to reprint portions of articles or whole articles must be obtained in writing. Please send editorial comments and requests for reprint permission to research.library@sf.frb.org