Financial executive pay is a convex function of profits if recipients get a greater increment in pay when returns are high as opposed to moderate, compared with when returns are moderate as opposed to low. Convex compensation packages give financial executives incentive to adopt risky investment projects, implement highly levered capital structures, and create new risk. Financial regulators may be able to enforce changes in compensation that would attenuate these adverse effects.
To varying degrees, most economists believe that economies perform better when markets are run largely independently of government than they do when government plays a dominant role. Economists have provided a range of formal arguments to support this conclusion. Of course, these arguments require assumptions, and the question is to what extent these assumptions are satisfied in the real world. This Economic Letter examines an important instance where the requisite assumption appears not to be satisfied.
The recent financial and economic crisis has led many to question the presumption in favor of private markets. Government agencies led by the U.S. Treasury Department and the Federal Reserve played an active role in attempting to mitigate the effects of the crisis. Some of the policy responses included injecting large sums of taxpayer money into the financial system. No one is enthusiastic about these actions, but to the extent that the alternative was a financial breakdown like that which occurred in the 1930s, measures along these lines were difficult to avoid.
Much of the public, perhaps a majority, has accepted the broad principle of an expanded role for government in response to the crisis. However, the use of taxpayer money to pay multimillion-dollar bonuses and award outsized options packages to senior executives and successful traders at institutions receiving government support, which includes most large financial institutions, has sparked widespread public revulsion. Partly this reaction reflects the perception that some institutions have been supported but others have not, creating a playing field that is no longer level. Without minimizing this consideration, broader issues are at stake. With a few exceptions, such as Blinder (2009), these issues have not been adequately discussed in the financial press.
Figure 1
The concept of convex compensation
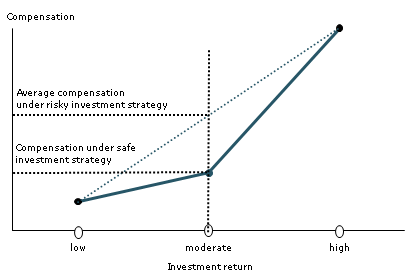
Large bonuses and options packages exemplify a phenomenon that economists know as “convex payoffs.” Mathematically, a convex function is one for which the line connecting any two points on the graph of the function lies on or above the graph (see Figure 1). For example, suppose that a trader can have a high return, a moderate return or a low return. The higher the trader’s return, the higher the trader’s pay. Pay is convex if the trader realizes a greater increment in pay when returns are high as opposed to moderate, compared with when returns are moderate as opposed to low.
What this means in practice is that bonuses and options packages have the property that the trader who does extremely well can look forward to a multimillion-dollar bonus but is not penalized millions of dollars when he or she does badly. Similarly, the recipient of an options package experiences a large windfall when the price of the company’s stock increases. But if the stock does extremely badly, he or she pays no penalty relative to the case when the stock drops modestly.
Markets do a good job of allocating resources in competitive settings, so that buyers and sellers individually cannot affect prices. In that case the payment for a given good or service is proportional to the amount transacted. Only under this condition can prices accurately communicate information about scarcity and desirability. Convex payoffs represent a departure from this principle. Payoffs are a nonlinear function of returns. As this argument suggests, convex payoff functions distort the incentives of financial practitioners. Specifically, they induce a motive to gamble. If paid according to a convex function, an executive may earn more money on average during a mixture of high revenue years and low revenue years than he or she would under a succession of moderate revenue years, even if average revenue is higher in the latter case. The executive is therefore motivated to adopt risky financial strategies. Sometimes these risks work out and sometimes they don’t. But high income in good years more than offsets low income in bad years.
The stockholders of financial firms—or, in cases in which government support is extended, taxpayers—have the opposite payoff. They benefit from a fraction of the gains, but bear all the losses. Therefore they may be made worse off by a risky investment strategy even if the strategy itself has favorable odds. Convex payoffs create what is called an “agency problem.” The executives have interests that diverge from those of the stockholders, for whom they are supposedly working.
Consequences of convex payoff functions
Many of the features of financial markets that have caused the most trouble recently are recognized as implications of the incentive to gamble induced by convex compensation packages.
Risky investments. We have learned over the past several years that private-label mortgage-backed securities are very risky. There was really never any doubt about this. The value of mortgages depends on price trends in housing, since house prices are a major determinant of mortgage defaults. House price changes are highly correlated, so there is not much opportunity to reduce risk by diversifying. In the past literally every housing price bubble eventually burst, so there was never much doubt that sooner or later there would be a day of reckoning for mortgage-backed securities. Nonetheless, market participants had every incentive to continue creating and acquiring these securities. At least for the moment, they were profitable, often highly so, meaning that they generated bonuses for everyone. After the bonus check cleared, market participants no longer had to worry about what happened to the securities. Of course, this is an oversimplification, but it illustrates the distortion of incentives that convex pay formulas create.
Leverage. Leverage magnifies the effects of risky investments on firmwide returns, an effect that is true in both directions. In extreme cases, such as those we have experienced in the past several years, taxpayers play a major role in creating convex payoff functions for investment banks. These institutions set up highly levered capital structures, typically on the order of 30 to 1, meaning that total assets were about 30 times greater than total capital. Both managers and stockholders did extremely well when returns were high. But when returns fell so low that bailouts were necessary, taxpayers footed the bill. Those bills were sometimes enormous because of the magnifying effect of leverage. The convex effect was more pronounced with investment banks than with commercial banks. Capital requirements and tighter regulatory regimes generally resulted in much lower leverage ratios of around 10 to 1 for commercial banks. Arguably even lower leverage ratios are needed to protect the position of taxpayers.
Creation of risk. As noted above, in the competitive model, financial markets allocate existing risk to those most willing to bear it. But, under convex payoffs, market participants do not wish to avoid risk, implying that they do not require compensation for bearing risk. Bring it on—the more, the better. Accordingly, not only will participants be motivated to bear risk, but markets will create new risky assets. The obvious example is credit default swaps, in which market participants make bets that particular bonds will or will not default. Such assets could be used as classical finance theory dictates to transfer default risk to those best able to bear it. But the extremely high volume of trade in such assets in recent years suggests that market participants were inst
ead using them to speculate on risks that they would not otherwise be exposed to. In other words, credit default swaps as actually used created risk. As Raghuram G. Rajan of the University of Chicago pointed out in 2005, before the current crisis, convex pay packages lead financial firms to introduce new risk rather than efficiently allocate existing risk. A possible objection to this line of reasoning is that if convex pay induces managers to take excessive risk, it ought to reduce the firm’s value. Why do stockholders not take action to remove the distorted incentives so as to increase stock value? This is an important and difficult question. The answer may be that when stock ownership is highly dispersed, as it usually is with large financial firms, no individual owner has either the incentive or the ability to discipline managers. Also, pressure to hire and retain high-quality managers necessitates paying high average salaries. Given the inappropriateness of paying high salaries during years when performance is poor, it may be that the only way to pay high average salaries is to adopt convex payoff schedules.
Conclusion
There is not much evidence that financial markets are in any hurry to discard convex pay, but there are some signs of change. Recently some financial institutions have said they are considering delaying payout of bonuses awarded on the basis of successful performance. Under these proposals, if the successes of a given year are reversed in later years, the bonus is canceled. This reform obviously mitigates the incentive to gamble and, hopefully, motivates market participants to develop long-term value rather than engage in speculation that is only briefly profitable.
The regulatory system, including the Federal Reserve, is currently implementing guidelines designed to mitigate the problems discussed in this Letter. However, there is no consensus on the question of how much government intervention in the determination of compensation is appropriate. It remains to be seen whether the new regulations will substantially improve the situation. (See Shiller 2010 for a discussion of regulation as it relates to convex payoffs.)
References
Blinder, Alan. 2009. “Crazy Compensation and the Crisis.” The Wall Street Journal, May 28.
Rajan, Raghuram G. 2005. “Has Financial Development Made the World Riskier?” NBER Working Paper 11728.
Shiller, Robert J. 2010. “Help Prevent A Sequel: Delay Some Pay.” New York Times, June 21.
Opinions expressed in FRBSF Economic Letter do not necessarily reflect the views of the management of the Federal Reserve Bank of San Francisco or of the Board of Governors of the Federal Reserve System. This publication is edited by Anita Todd and Karen Barnes. Permission to reprint portions of articles or whole articles must be obtained in writing. Please send editorial comments and requests for reprint permission to research.library@sf.frb.org