Estimating market expectations for inflation from the yield difference between nominal Treasury bonds and Treasury inflation-protected securities—a difference known as breakeven inflation—is complicated by the liquidity differential between these two types of securities. Currently, the extent to which liquidity plays a role in determining breakeven inflation remains contentious. Information from the market for inflation swaps provides a range for the possible liquidity premium in TIPS, which in turn suggests a range for estimates of inflation expectations that is well below the widely followed Survey of Professional Forecasters inflation forecast.
Measures of inflation expectations are important both for the conduct of monetary policy and for assessing its credibility. One way of determining inflation expectations is to look at the yield difference between traditional Treasury securities and Treasury inflation-protected securities (TIPS) of the same maturity, known respectively as nominal and real Treasury yields. This difference indicates the breakeven inflation rate, the level of inflation at which investments in both kinds of securities would be equally profitable for a given maturity. Breakeven inflation rates provide particularly useful measures of inflation expectations because they are available at a high frequency for a wide range of time horizons.
However, using breakeven inflation rates as measures of inflation expectations can be problematic. In addition to the expected inflation component, breakeven inflation is governed by two unobservable factors: the premium that bond investors are willing to pay for protection against the risk that inflation will overshoot its expected path and the higher yield they require for holding relatively less liquid TIPS. The inflation risk factor pulls the observed TIPS yields down relative to nominal bonds, causing breakeven inflation to be correspondingly high. The liquidity factor pushes observed TIPS yields up, bringing breakeven inflation down. The yield premiums associated with both factors vary over time and often in offsetting ways, making it difficult to capture the residual expectations component of the breakeven inflation rate.
In this respect the usefulness of breakeven inflation for assessing inflation expectations depends on the relative importance of the inflation overshoot and liquidity risk factors, and the modeling techniques used to separate out these risk factors from the expectation component. Currently, the extent to which the liquidity differential between nominal and real Treasury bonds affects pricing remains a point of contention, causing some to question the reliability of the models used to extract inflation expectations from Treasury yields. Thus, determining the liquidity premium in TIPS pricing is an important step in improving such models and achieving more accurate measures of inflation expectations.
In this Economic Letter, we utilize the maximum range for the TIPS liquidity premium described in Christensen and Gillan (2011) to adjust observed real yields for potential liquidity effects. We demonstrate how this bound converts into a maximum range for the estimated inflation expectations using a model of nominal and real Treasury yields. Estimates from the model and empirical evidence from the secondary TIPS market indicate bond investors’ inflation expectations are most likely near the lower end of the maximum range. This suggests that the estimates of inflation expectations from D’Amico, Kim, and Wei (2010) and the Survey of Professional Forecasters are too high.
The admissible range for expected inflation
To get a handle on the potential magnitude of the liquidity effects in observed TIPS yields, we use the model-independent maximum range for the TIPS liquidity premium (Christensen and Gillan 2011). This range is constructed by subtracting breakeven inflation from the inflation swap rate for the comparable maturity. Given realistic assumptions about the relative liquidity of nominal Treasuries, TIPS, and inflation swaps, the range provides a bound to the TIPS liquidity premium. The difference between breakeven inflation and the comparable swap rate then represents the sum of trading frictions in both the inflation swap and TIPS markets. Identifying where the premium falls within the range is difficult. But, by considering the two extremes of the range, we can account for all possible variation in the TIPS liquidity premium. The lower bound of the range is zero because we assume TIPS to be less liquid than nominal Treasuries. This lower extreme represents the case where the liquidity of nominal Treasuries and TIPS are the same. If the TIPS liquidity premium is at the upper bound, then the opposite is the case and inflation swaps are unaffected by liquidity factors.
Figure 1
TIPS liquidity premium:
Maximum range and D’Amico et al. estimate
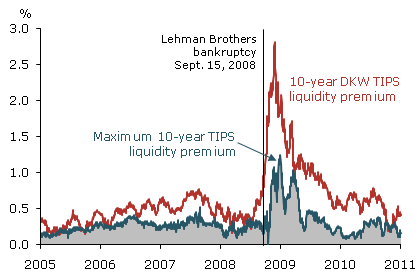
Figure 1 shows the maximum TIPS liquidity premium at the 10-year maturity in blue, with the admissible range shaded in gray underneath. The range grew substantially during the crisis, indicating the level of the TIPS liquidity premium was potentially substantial at the time, while the upper bound was considerably lower during the rest of the period.
A few researchers have tried to estimate the TIPS liquidity premium directly and use these results to adjust estimates of inflation expectations. The model described in D’Amico et al. (2010) estimates the liquidity premium in TIPS yields explicitly to extract measures of expected inflation. Figure 1 compares the maximum 10-year TIPS liquidity premium to the corresponding D’Amico et al. estimate, labeled DKW. The DKW TIPS liquidity premium is almost always above the admissible range, indicating that their estimate is generally inconsistent with pricing information from the TIPS and inflation swap markets.
Instead of attempting to identify the TIPS liquidity premium explicitly as in the D’Amico et al. approach, we propose using our range to maximally correct TIPS yields for liquidity and then estimate a model at the natural extremes of the resulting range for real yields. In other words, we perform two model estimations. The first uses real yields as observed, implying there is no liquidity premium in TIPS. The second uses liquidity-corrected yields produced by deducting the upper bound of the admissible range from observed TIPS yields. (See the model of nominal and real yields developed in Christensen, Lopez, and Rudebusch 2010 and Christensen 2008.)
Figure 2
Estimates of expected inflation and SPF forecast
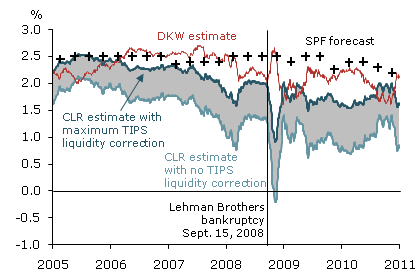
Figure 2 shows 10-year inflation expectations for the two scenarios using the Christensen et al. model, labeled as CLR. The dark blue line represents the expected inflation that results from correcting real yields with the maximum admissible liquidity premium. The light blue line corresponds to no liquidity correction. The gray range in between tracks one-for-one the maximum TIPS liquidity premium range in Figure 1. If the TIPS liquidity premium is actually near the upper bound, then the correction to the observed TIPS yields would be large. This means that frictionless TIPS yields that are not biased by liquidity factors would be correspondingly low. As a result, liquidity-adjusted breakeven inflation would be higher than the observed rate, implying higher estimates for expected inflation. Conversely, a liquidity premium near the zero lower bound of the range results in lower estimates for inflation expectations.
Correcting TIPS yields for liquidity in this manner limits the set of admissible estimated inflation expectations and allows us to compare the range of liquidity-adjusted estimates from the Christensen et al. model with other commonly used measures. Figure 2 plots the corresponding estimate from the D’Amico et al. model (thin red line) in addition to the quarterly Survey of Professional Forecasters (SPF) inflation forecasts for the same horizon. Both series tend to be above the admissible range of expected inf
lation from the Christensen et al. model. As Figure 1 shows, the D’Amico et al. model overcorrects for liquidity for much of the period before and after the onset of the financial crisis, leading to elevated estimates of expected inflation. The Survey of Professional Forecasters typically produces even higher expected inflation values and is notably insensitive to the output declines that occurred following the collapse of Lehman Brothers.
How big is the TIPS liquidity effect?
As we have shown, the D’Amico et al. estimate of expected inflation may be based on TIPS liquidity effects that are too large. Yet the admissible range of TIPS liquidity effects allows for a relatively wide window of inflation expectations estimates. Examining model-implied deflation probabilities during the recent financial crisis supplies an opportunity for determining where the TIPS liquidity effect might fall within the admissible range. The high expected inflation at the top of the range converts into a low probability of deflation while the bottom of the range implies greater deflationary risk. This has implications for the market value of deflation protection embedded in TIPS.
In addition to indexing the principal to the consumer price index, TIPS also guarantee the nominal value of the principal if there is net deflation over the bond’s life. The value of this deflation protection is best illustrated by comparing two TIPS securities of comparable maturity dates where the option is valuable for one of the securities but not for the other. Based on the work of Christensen, Lopez, and Rudebusch (2011), we calculate the five-year par-coupon yield of a seasoned TIPS that has accrued enough inflation compensation to make the payout at maturity almost certainly higher than the original principal amount. In this case, the deflation protection has no value since any deflation would only eat into the accrued inflation compensation. We compare this with the five-year par-coupon yield of a newly issued TIPS with zero accrued inflation compensation, meaning that deflation risk can significantly affect its pricing.
The dashed black line in Figure 3 represents the observed yield difference between seasoned and newly issued TIPS of comparable maturities. Until the failure of Lehman Brothers, the yield spread was typically negative because deflation risk was negligible. However, in the weeks and months following the Lehman failure, a significant and persistent spread between yields developed between seasoned and newly issued TIPS that reflected widespread deflation fears. This spread has only recently returned to near pre-crisis levels as deflation fears have waned.
Figure 3
Yield spread of seasoned over newly issued TIPS
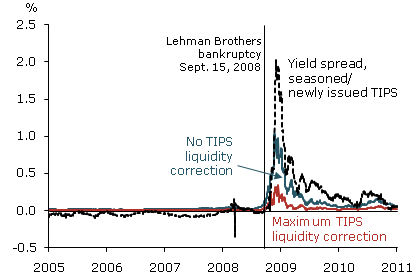
In Figure 3, the blue and red lines represent the model-implied yield spread between such pairs of TIPS when expected inflation is respectively at the minimum and maximum of the admissible range. At the maximum level of expected inflation, the yield spread is far below the observed level. At the minimum, the model generates results that are more consistent with the observed data. This suggests that the unobserved TIPS liquidity premiums are most likely near the lower end of the admissible range. It follows that if inflation expectations were actually at the levels suggested by D’Amico et al. or the Survey of Professional Forecasters, they would imply a value to deflation protection that would be further below the observed spread than the red line because the deflation probability would be even more trivial at those levels of expected inflation.
Conclusion
Until a greater consensus emerges on the role of liquidity in TIPS pricing, it is important to analyze the sensitivity of inflation expectations derived from the breakeven rate to variation in the assumed TIPS liquidity premium. Correcting TIPS yields prior to estimation using the admissible range demonstrated here provides a simple way to determine this sensitivity. Furthermore, the range can be used as a metric to assess more direct estimates of TIPS liquidity effects. Our evidence suggests that the actual TIPS liquidity premium is likely to be towards the lower end of the admissible range. If so, our model-based estimates of expected inflation suggest that the inflation expectations of bond investors are well below the widely followed Survey of Professional Forecasters inflation forecast.
Reference
Christensen, Jens H. E. 2008. “Treasury Bond Yields and Long-Run Inflation Expectations.” FRBSF Economic Letter 2008-25 (August 15).
Christensen, Jens H. E., and James M. Gillan. 2011. “Has the U.S. Treasury Benefited from Issuing TIPS?” FRBSF Economic Letter 2011-12 (April 18).
Christensen, Jens H. E., Jose A. Lopez, and Glenn D. Rudebusch. 2010. “Inflation Expectations and Risk Premiums in an Arbitrage-Free Model of Nominal and Real Bond Yields.” Journal of Money, Credit, and Banking 42(6) , Supplement, pp. 143—178.
Christensen, Jens H. E., Jose A. Lopez, Glenn D. Rudebusch. 2011. “Extracting Deflation Probability Forecasts from Treasury Yields.” FRBSF Working Paper 2011-10.
D’Amico, Stefania, Don H. Kim, and Min Wei. 2010. “Tips from TIPS: The Informational Content of Treasury Inflation-Protected Security Prices.” Finance and Economics Discussion Series 2010-19, Federal Reserve Board.
Opinions expressed in FRBSF Economic Letter do not necessarily reflect the views of the management of the Federal Reserve Bank of San Francisco or of the Board of Governors of the Federal Reserve System. This publication is edited by Anita Todd and Karen Barnes. Permission to reprint portions of articles or whole articles must be obtained in writing. Please send editorial comments and requests for reprint permission to research.library@sf.frb.org