The performance of the residential housing market over the last ten years has been remarkable. According to the Office of Federal Housing Enterprise Oversight (OFHEO), house prices have appreciated at an annual rate of 5.4% on average (68.9% over the whole time period).
The performance of the residential housing market over the last ten years has been remarkable. According to the Office of Federal Housing Enterprise Oversight (OFHEO), house prices have appreciated at an annual rate of 5.4% on average (68.9% over the whole time period). Perhaps even more remarkable is that the performance was strong even when economic activity overall was weak. Average annual appreciation rates have been 7.4% (26% in total) since the collapse of the Nasdaq in 2000 and 7.1% (20% in total) since 2001:Q1, the beginning of the 2001 recession. In contrast, since the start of the 2001 recession, the S&P 500 and Nasdaq have averaged negative annual returns of –2.43% and –1.42% respectively.
These kinds of statistics have generated an enormous amount of commentary along with suspicions of a house price bubble. At first glance, housing would appear to be just the type of market that is susceptible to systematic mispricings. Most market participants have little experience, making transactions only infrequently. Asymmetric or incomplete information between buyers and sellers about demand and prices is acute. Even with the advent of new technologies, the matching of buyers with sellers remains cumbersome and slow. And unlike other markets, there are no good ways to “short” the housing market if prices get too high.
This Economic Letter describes one of the measures commonly used to gauge the fundamental value of housing—the price-rent ratio. We describe the kinds of forces that cause the ratio to move over time and document which forces appear to be most important. We document the way that the housing market typically adjusts to changes in economic fundamentals.
Fundamental value and the price-rent ratio
The price of housing is determined by the forces of supply and demand for the housing good. So, naturally, many economists try to relate prices to variables that might shift supply and demand, like interest rates and household income. Price dynamics are often described in terms of the interactions between these variables and the natural constraints on delivering new supply to the market (see McCarthy and Peach 2004).
We borrow from the finance literature to take a different approach. The finance paradigm holds that an asset has a fundamental value that equals the sum of its future payoffs, each discounted back to the present by investors using rates that reflect their preferences. For stocks, the payoffs requiring discounting are the expected dividends. This approach can extend to housing by recognizing that a house yields a dividend in the form of the roof over the head of the occupant. The fundamental value of a house is the present value of the future housing service flows that it provides to the marginal buyer. In a well-functioning market, the value of the housing service flow should be approximated by the rental value of the house.
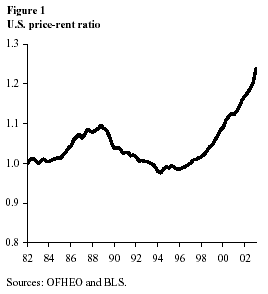A bubble occurs—in either the stock market or the housing market—when the current price of an asset deviates from its fundamental value. Right away we see that bubbles are difficult to detect because fundamental value is fundamentally unobservable. No one knows for sure what future dividends are going to be, or what discount rates investors will require on assets. Despite this obstacle, analysts still find it helpful to construct measures of fundamental value for comparison to actual valuations. One popular measure is the price-dividend ratio, which corresponds to a price-rent ratio for houses. The price-rent ratio for the U.S. housing market is in Figure 1. The price series is the existing home sales price index published by OFHEO; this index is a repeat sales index, meaning that index changes are compiled from the price changes on individual houses that turn over during the sample period. One of its drawbacks is that it does not fully differentiate between pure house price appreciation and price changes due to depreciation or home improvement. The rent series is the owner’s equivalent rent index published by the Bureau of Labor Statistics (BLS); this series is intended to measure changes in the service flow value of owner-occupied housing. The figure suggests that current prices are high relative to rents. More precisely, house prices have been growing faster than implied rental values for quite some time: currently, the value of the U.S. price-rent ratio is 18% higher than its long-run average.
It is tempting to identify a bubble as a large and long-lasting deviation in the price-rent ratio from its average value, just like the one that we see in Figure 1. But exactly how large and how long-lasting a deviation must be to resemble a bubble is far from obvious. There is no reason to believe that a price-dividend ratio should be constant over time, even in the absence of bubbles; in particular, Campbell and Shiller (1988) showed that the value of the ratio today can increase only if there are expected future increases in dividends, expected future decreases in returns, or both. This simple model of the price-dividend ratio is based on a simple identity and the definition of a return as the sum of a dividend yield and a capital gain/loss.
To make the implications of this simple model more concrete for our housing application, imagine a real estate market near a military base that has just been scheduled to close five years from now. The inevitable job loss associated with the closure is an adverse shock to the demand for housing. This should cause a decrease in the future value of the housing dividends on houses in the area, driving house prices down immediately. Current rental contracts, however, should be relatively unaffected because the closure is so far off in the future. Thus, the price-rent ratio should decline. Alternatively, suppose the government could credibly promise to reduce taxes on real estate and keep them low forever. This change would probably lead to a higher demand for housing; at the margin, households would have the incentive to shift savings from financial assets to housing. In addition, the elimination of uncertainty about future tax rates would imply that houses are safer assets, requiring lower future returns. In this case, the price-rent ratio should increase.
What moves the price-rent ratio?
Given a notion of the sources of variability in the price-rent ratio, it is natural to wonder which sources are most important. Cochrane (1991) conducts this exercise for the case of stocks and finds that most of the most variation comes from changes in returns.
We conduct Cochrane’s experiment for houses. To construct the price-rent ratios we use OFHEO’s existing home sales index and the owner’s equivalent rent index published by the BLS. We use quarterly data, ranging from 1982:Q4 to 2003:Q1. The constraint on the sample period is that the owner’s equivalent rent series does not begin until 1982. We could extend the rental series back further by using a pure rent series, but only at the cost of severing the link between an owner-occupied price in the numerator of our ratio and an approximation to an owner-occupied service flow value in the denominator.
The basic insight of the empirical research on price-dividend ratios is that movements in the price-dividend ratio can be decomposed into two parts: movements relative to future expected dividend growth rates, and movements relative to future expected returns. In theory, these future variables are unknown to the investors when they set prices. In this application, we set the expected future dividend growth rates and returns equal to the actual values that occurred. Also in theory, we should assume all “future” dividend growth rates and returns to mean those extended to infinity. Obviously, this is not possible, so we study how the price-rent ratio moves relative to the next 15 quarters of rental growth rates and returns. (We experimented with other horizons, and found that the results did not change much.) Note also that we are unable to incorporate the current episode of price appreciation. We run out of observations before we can say anything definitive about the recent house price appreciation.
The main result from this decomposition is that the behavior of the price-rent ratio for housing mirrors that of the price-dividend ratio for stocks. The majority of the movement of the price-rent ratio comes from future returns, not rental growth rates. This will not comfort everyone, as it implies that price-rent ratios change because prices are expected to change in the future, and seemingly out of proportion to changes in rental values. A more comforting conclusion, however, is that, despite the well-known frictions in real estate markets, the dynamics of a common valuation measure are still similar to those observed in a near-frictionless market like the stock market. It may appear that returns are quite volatile relative to changes in rental values, but this is true for stock prices as well and only serves to underscore our inability to understand how expectations and required rates of return on assets are formed.
Another result is that almost all of the movement in the aggregate U.S. price-rent ratio was accounted for by two factors—the proxy for future growth in rents and the proxy for future returns. Put another way, other factors, such as bubbles, do not appear to be empirically important for explaining the behavior of the aggregate price-rent ratio. At the same time, when applied to local real estate markets, in many cases the movement in the price-rent ratio predicted by the model is much greater than the actual movement; specifically, the results indicate that something other than our measures of future rent growth and returns explains price-rent ratios. While we do not know what this “something other” is, the more common overstatement of volatility is caused by a much stronger comovement between the price-rent ratio and future returns than the comovement between price-rent and future rent growth.
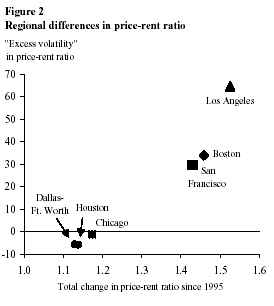The excess of the price-rent ratio volatility (the difference between the movement predicted by the model and the actual movement) can be traced to the volatility of house prices in local markets. Most recently, local housing markets that historically have had “excess” volatility in future returns also exhibit high house prices compared to fundamentals. This is shown in Figure 2, where the vertical axis measures the excess volatility in percent terms; zero corresponds to the case in which the model and our implementation explain the actual price-rent ratio precisely. The horizontal axis measures the price-rent ratios normalized to have the value of one in 1995:Q4.
The figure shows that in some markets, such as Dallas and Chicago, the combination of future growth in rents and future returns account for most of the variation in the price-rent ratio. Price-rent ratios in these markets appear to behave as do those in the national market. Other markets, such as Boston, Los Angeles, and San Francisco, have return streams that are much more variable than the price-rent ratios they are supposed to be tied to. Perhaps not coincidentally, these markets are thought to be ones where the supply constraint on new construction is particularly tight. Also, these are markets that now appear to be most highly valued.
The price-rent ratio for the U.S. and many regional markets is now much higher than its historical average value. We used a model from the finance literature to describe how the price-rent ratio can move over time. We found that most of the variance in the price-rent ratio is due to changes in future returns and not to changes in rents. This is relevant because it suggests the likely future path of the ratio. If the ratio is to return to its average level, it will probably do so through slower house price appreciation.
John Krainer
Economist
Chishen Wei
Research Associate
Campbell, J., and R. Shiller. 1988. “The Dividend-Price Ratio and Expectations of Future Dividends and Discount Factors.” Review of Financial Studies 1, pp. 195–227.
Cochrane, J. 1991. “Explaining the Variance of Price-Dividend Ratios.” Review of Financial Studies 5(2), pp. 243–280.
McCarthy, J., and R. Peach. 2004. “Are Home Prices the Next ‘Bubble’?” FRBNY Economic Policy Review. http://www.newyorkfed.org/research/epr/04v10n3/0412mcca.html
Opinions expressed in FRBSF Economic Letter do not necessarily reflect the views of the management of the Federal Reserve Bank of San Francisco or of the Board of Governors of the Federal Reserve System. This publication is edited by Anita Todd and Karen Barnes. Permission to reprint portions of articles or whole articles must be obtained in writing. Please send editorial comments and requests for reprint permission to research.library@sf.frb.org