A new proposal by the Basel Committee on Banking Supervision for setting the amount of capital banks must hold against potential losses from interest rate risk uses only a few, very stylized scenarios. Analysis shows the proposed scenarios are extremely unlikely to occur. While they may be appropriate for setting bank capital guidelines, they are much less relevant for everyday risk management. Instead, using a modeling framework with a plausible range of interest rate scenarios would be more relevant to help banks manage their interest rate risk.
One of the main risks banks must account for is interest rate fluctuations, along with the associated changes in the values of their assets and liabilities. While interest rate risk is certainly more immediate for marketable securities such as government or corporate bonds, other assets and liabilities that are not generally marked-to-market each day are also subject to interest rate risk. The Basel Committee on Banking Supervision has proposed setting bank capital guidelines for this risk according to some stylized techniques (see BCBS 2015). In this Economic Letter, we assess some of these proposals in the context of the probability-based stress-testing framework developed by Christensen, Lopez, and Rudebusch (2015). We find that the BCBS proposals can provide some basic insights into managing interest rate risk and might be appropriate for setting regulatory capital standards. However, since they emphasize unlikely interest rate scenarios, these proposals have important limitations when compared with more comprehensive interest rate modeling and risk management techniques.
Interest rate risk in the banking book
In general, banks hold assets like mortgages and liabilities like deposits in their “banking book.” These are balance sheet items that are subject to accrual accounting standards, as opposed to market-based accounting. While the banking book need not account for interest rate fluctuations directly, there remains some underlying risk. In June 2015 the BCBS proposed two options for how regulators might set regulatory capital requirements for this risk: a standardized approach based on a series of regulatory calculations and an approach based on banks’ own risk models.
We focus our analysis on the standardized approach, which uses specific interest rate scenarios to evaluate a firm’s banking book. The potential losses implied by these scenarios would help determine the firm’s capital requirements. We assess two of the main scenario types in the proposal. First, we examine parallel moves of the entire yield curve by a set number of basis points, that is, hundredths of a percentage point. Given that U.S. short-term rates are near the zero lower bound, we consider only upward shifts of the yield curve. The second set of scenarios is based on shifting the slope of the yield curve. The BCBS uses the term “flattener” to correspond to scenarios in which longer-term rates decline by as much or more than short-term rates rise. This combination of changes causes the slope of the yield curve to decline, and thus the curve becomes flatter. Conversely, the term “steepener” corresponds to scenarios that have long-term rates rising by as much as or more than short-term rates decline. Again, due to current low short-term rates, we assess only those scenarios that represent a flattening of the yield curve.
The interest rate risk insights derived from these two types of scenarios are complementary. The parallel shift scenarios provide insights into how a common rise in interest rates would affect a firm given its funding strategy, for example paying higher rates on deposits, and the duration of its loan portfolio, for example the sensitivity of loan values to interest rate changes. Slope scenarios provide more insight into the risks to banks from differential repricing of assets and liabilities. For example, flattening scenarios show the interest rate gap that arises when the rates banks pay on short-term liabilities rise faster than the rates they receive on longer-term loan assets. The numerical insights from applying these scenarios give bank risk managers information on the greatest sensitivities to interest rate changes and how to reduce them if needed.
However, one important element missing from these scenarios that limits their usefulness is knowing how likely they are to occur, as noted in Christensen et al. (2015). Using a method that assesses not only potential yield curve changes but also incorporates the likelihood of various interest rate changes should provide a more comprehensive approach to managing interest rate risk.
The assessment framework
We base our assessment of the scenarios on the Christensen et al. (2015) framework, which itself is based on the class of yield curve models originally developed by Christensen, Diebold, and Rudebusch (2011). These are models of the term structure of U.S. Treasury zero-coupon yields that use three dynamic factors to characterize different elements of the yield curve. The “level” factor affects yields of all maturities in a similar way and is mainly responsible for upward or downward shifts in the yield curve. This factor is most closely related to the parallel BCBS scenarios. The “slope” factor affects the slope of the yield curve by moving short- and long-term rates in opposite directions, which relates to the BCBS steepener and flattener scenarios. The third factor, known as “curvature,” is primarily responsible for bends in the yield curve as it affects medium-term yields in the opposite direction as both short- and long-term yields.
Using an enhanced model from Christensen and Rudebusch (2015a, b), Christensen et al. (2015) projected 10,000 possible Treasury yield curves. From that, they were able to forecast the probability of various outcomes for the Federal Reserve’s securities holdings. For example, they found that, as of June 2014, the probability that the Fed’s portfolio of nominal Treasury bonds would decline below its face value was about 5% over the next year and close to 25% over three years.
Assessing the BCBS scenarios
We use the framework outlined above to assess the likelihood of the proposed BCBS scenarios occurring. We set the date of analysis as June 25, 2014, as in Christensen et al. (2015), and the period for the scenario to occur as six months, although we examine longer holding periods as well. We then generate 50,000 simulations to ensure that the tails of the yield distributions are well represented.
To start, the red line in Figure 1 plots the probability of a 100 basis point (1 percentage point) yield increase over a six-month period from our starting date for each maturity point along the yield curve. For example, the three-month yield, the left-most point, would increase by 100 basis points in 7.5% of our 50,000 yield curve simulations. Except for a slight bump near the three-year maturity caused by curvature risk, the probabilities of such a yield increase decline gradually until the 20- year maturity, which has a 0.25% probability. Note that these are probabilities of yield increases at each point on the term structure and not that of a common move across all maturity points. The probability of a common move across all maturities would be within the range of these individual probabilities—near 0–8% for the 100 basis point gain—with a strong tendency toward the lower end.
Figure 1
Probabilities for different yield increase scenarios
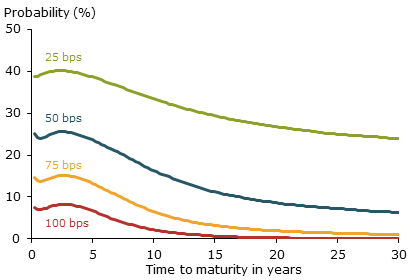
Note: Lines show the probability for an increase in the yield at each individual maturity by at least the stated number of basis points (bps).
Looking closer at the figure, consider the probability of a 100 basis point increase at the 10-year maturity, which is 2.1%. For that same maturity, yield increases of 25, 50, and 75 basis points, would have probabilities of 33.5%, 16.3%, and 6.5%, respectively. The strength of this kind of probability-based stress-testing framework is that it provides a more comprehensive view of possible interest rate moves and their likelihoods. In addition, it allows us to readily generate the value-at-risk estimates often used to manage bank exposure to market risks (see BCBS 2011). In our exercise, an interest rate risk manager interested in a 10-year yield change corresponding to a 5% probability could determine that an 84 basis point increase would be the appropriate threshold.
Focusing on the parallel scenario, Figure 2 plots the joint probability of a minimum increase of 100 basis points in both the short-term rate (three-month Treasury yield) and the long-term rate (30-year Treasury yield), as well as milder parallel increases of 25, 50, and 75 basis points for various holding periods. The probability framework allows us to examine holding periods other than the six months recommended by the BCBS, so the figure presents probabilities for periods of up to three years. The probability of a +100 basis point parallel shift rises steadily from less than 1% at the six-month horizon to 12% at the three-year horizon. The BCBS recommends using this scenario with a holding period of six months to set regulatory capital requirements, but based on our simulated probabilities this scenario is quite unlikely to occur. Instead, the fuller assessment would provide a more nuanced measure of a firm’s interest rate sensitivities. For example, the probability of a +50 basis point parallel shift (blue line) rises from 4.3% to 28.5%, which might be more relevant to consider for calibrating regulatory capital.
Figure 2
Probabilities of parallel shift scenarios by basis points
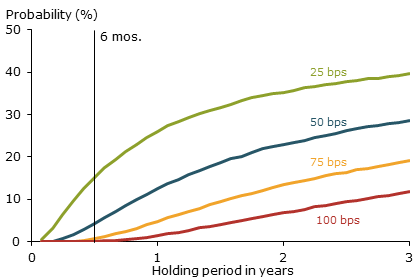
Note: Lines show the probability for an increase of at least the stated number of basis points (bps) in both the short-term and long-term rates.
Turning to the BCBS flattener proposal, we again follow the guidelines and consider a scenario in which the three-month Treasury yield increases a minimum of 100 basis points, while the 30-year Treasury yield decreases by at least the same amount. Figure 3 shows the probabilities of this scenario for several holding periods as well as those of milder flattening scenarios with yield change thresholds of 25, 50, and 75 basis points. Focusing on the 100 basis point scenario at the six-month horizon, the proposed BCBS scenario has a nearly zero—0.07%—chance of occurring within our simulation, and thus provides very limited information for calibrating regulatory capital or for broader interest rate risk management. Using the more complete probabilistic approach, the figure shows that a 25 basis point flattener scenario would likely be more useful at the six-month horizon as it has a nearly 1.5% chance of occurring. Similarly, a risk manager could see that the interest rate scenarios that have approximately 5% chance of occurring are a 25 basis point flattener at a one-year horizon and a 50 basis point flattener at a horizon of 2.5 years.
Figure 3
Probabilities of flattened yield curve scenarios
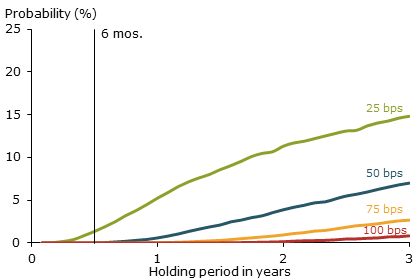
Note: Lines show the probability for an increase in the short-term rate of at least the stated number of basis points (bps) and a decrease in the long-term rate by at least the same amount.
Conclusion
The Basel Committee on Banking Supervision has proposed two methods to set regulatory capital requirements for banks’ interest rate risk exposures within the banking book: a standardized approach based on a series of regulatory choices, including a set of specified interest rate scenarios, and approaches based on banks’ own risk modeling efforts. Our analysis using a framework developed by Christensen et al. (2015) to incorporate the likelihood of certain scenarios suggests that the scenarios specified by the BCBS are very unlikely to occur. In that regard, our results could help guide policymakers in determining whether the proposed standards meet the stated goal of setting “appropriate capital to cover potential losses from exposures to changes in interest rates.” More generally, risk analysis based on a more complete modeling of scenarios provides a richer framework for setting bank capital standards and managing interest rate risk.
Jens H.E. Christensen is a research advisor in the Economic Research Department of the Federal Reserve Bank of San Francisco.
Jose A. Lopez is a vice president in the Economic Research Department of the Federal Reserve Bank of San Francisco.
References
Basel Committee on Banking Supervision. 2011. “Revisions to the Basel II Market Risk Framework.” Updated as of December 31, 2010, posted February 2011.
Basel Committee on Banking Supervision. 2015. “Interest Rate Risk in the Banking Book: Consultative Document.” June.
Christensen, Jens H.E., Francis X. Diebold, and Glenn D. Rudebusch. 2011. “The Affine Arbitrage-Free Class of Nelson-Siegel Term Structure Models.” Journal of Econometrics 164(1), pp. 4–20.
Christensen, Jens H. E., Jose A. Lopez, and Glenn D. Rudebusch. 2015. “A Probability-Based Stress Test of Federal Reserve Assets and Income.” Journal of Monetary Economics 73, pp. 2–43.
Christensen, Jens H.E., and Glenn D. Rudebusch. 2015a. “Estimating Shadow-Rate Term Structure Models with Near-Zero Yields.” Journal of Financial Econometrics 13(2), pp. 226–259.
Christensen, Jens H.E., and Glenn D. Rudebusch. 2015b. “Modeling Yields at the Zero Lower Bound: Are Shadow Rates the Solution?” Advances in Econometrics 35, forthcoming.
Opinions expressed in FRBSF Economic Letter do not necessarily reflect the views of the management of the Federal Reserve Bank of San Francisco or of the Board of Governors of the Federal Reserve System. This publication is edited by Anita Todd and Karen Barnes. Permission to reprint portions of articles or whole articles must be obtained in writing. Please send editorial comments and requests for reprint permission to research.library@sf.frb.org