How well stress tests measure a bank’s ability to survive adverse conditions depends on the statistical modeling approach used. Banks can access data on loan characteristics to precisely estimate individual default risk. However, macroeconomic scenarios used for stress tests—as well as the reports banks must provide—are for a bank’s entire portfolio. So, is it better to aggregate the data before or after applying the model? Research suggests a middle-of-the-road approach that applies models to data aggregated at an intermediate level can produce accurate and stable results.
Under the Dodd-Frank Act of 2010, U.S. banks must estimate their ability to survive various adverse macroeconomic and financial market shocks, a process known as stress testing. In these tests, banks often forecast potential losses using data from underlying portfolios at the individual loan level, but must report the outcome of the analysis at the aggregate level. This poses a question: Is it better to aggregate the data before it is analyzed, or is it better to study loan-level data and then aggregate the results?
In this Letter we summarize our recent research on stress testing. We show that, for portfolios of home equity lines of credit, an intermediate level of aggregation produces the best results. In particular, aggregating loan-level data to analyze at the county level produces accurate, stable, and conservative results. While this finding might not work for other types of loan portfolios, we draw two useful insights that can apply more broadly. First, when disaggregated data are available, model developers should consider the level of aggregation carefully. Second, intermediate levels of aggregation could provide a useful way to construct challenge models to ensure existing approaches are appropriate.
Bank stress testing process
Each year, the Federal Reserve creates a set of hypothetical scenarios for banks to use in stress tests to forecast their revenue, losses, and capital reserves for a range of financial and economic conditions. These scenarios include nine-quarter projections of aggregate variables for the U.S. and some foreign economies, such as GDP growth, inflation, interest rates, house prices, unemployment, and stock market prices. Banks then test how they would be affected in three types of scenarios: baseline, adverse, and severely adverse. Usually banks introduce these scenarios into their own forecasting models, linking macroeconomic variables to relevant outcomes for revenue and losses.
For example, banks can construct a loan-level, or “bottom-up,” model that predicts the probability of default on a home equity loan as a function of house prices, interest rates, and unemployment. The banks have data on each individual loan, such as the loan-to-value ratio and the borrower’s credit score and debt-to-income ratio. The banks also track the delinquency status of each loan. Thus, they can construct a loan-level model that would predict each loan’s probability of default. Similarly, they can construct statistical models that would allow them to predict bank losses if that borrower defaults. They can then aggregate all of the probabilities of default and subsequent expected losses to obtain total expected losses from home equity portfolios that they need to report for stress testing.
The difficulty arises because the probability of default on a particular loan depends on the price of a particular house and employment of a particular borrower at given point in time. However, similar information is not generally available for the stress testing scenarios. Although some scenarios can be refined to reflect county- and state-level factors, it is simply not feasible to produce variables for each U.S. borrower and each house. Thus, in the loan-level models used for stress testing, macroeconomic conditions can only be used as proxies for the variables that actually affect the probability of default. What is particularly problematic is that the resulting measurement error can make individual loans less sensitive to how macroeconomic factors may affect their default probability and therefore create insufficient differences between baseline and stress scenarios.
Alternatively, banks can use information on the aggregate default frequency in their entire home equity loan portfolio and evaluate how this frequency reacts to changes in the macroeconomic conditions. Such “top-down” models can then also be used to predict losses in stress scenarios (see Hirtle et al. 2015). The most important drawback of top-down models is that they are not able to account for changes in the portfolio composition and do not make full use of the heterogeneity in the data that could help produce more precise estimates of the relationships between different variables. (See Frame, Gerardi, and Willen (2015) for a cautionary lesson on the potential for supervisory errors during periods of portfolio composition change.)
Middle of the road?
The question that naturally arises when considering these two types of models is whether there is an intermediate level of aggregation between bottom-up and top-down models that could be useful. One way to think about this is by considering the example of home equity loans. Since information on two important determinants of default on these loans—housing prices and unemployment—are available at the county level, one could aggregate loan-level information to a county level, conduct statistical analysis on a panel of counties, and then aggregate predicted losses for stress testing purposes. This approach may have an advantage of mitigating measurement errors in macroeconomic factors while still allowing changes in geographical composition of the loan portfolio to have an effect.
Our research in Hale, Krainer, and McCarthy (2015) uses information on home equity lines of credit from CoreLogic to compare the performance of the models at different levels of aggregation. In this Letter we will focus on three different aggregation levels: loan-level, county-level, and top-down. For each of these, we estimate the models of default probability or expected default rate as a function of macroeconomic variables and loan characteristics, such as the borrower’s credit score and debt-to-income ratio, the loan-to-value ratio, and the year of loan origination. To simplify the analysis, we consider a loan to be in default when it becomes 90 days delinquent. For the aggregate models, we compute averages for loan characteristics.
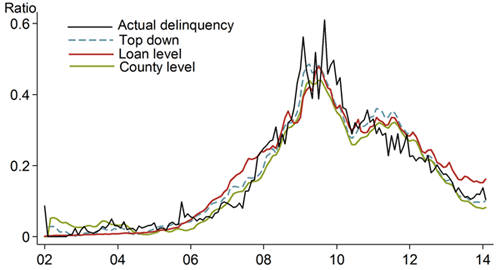
We evaluate the model’s performance using two main approaches: in-sample fit of the model evaluates how well the model describes the data, while out-of-sample fit of the model indicates how useful the model can be for forecasting purposes. To evaluate in-sample fit, we estimate the model using all available data and then compare the model predictions to actual outcomes. Figure 1 shows the in-sample fit of the loan-level, county-level, and top-down models of the probability of default on home equity lines of credit. The predicted default probabilities from all three models track the actual default rate very closely.
Figure 1
In-sample predictions for default probability vs. actual outcomes
To evaluate the out-of-sample fit of the model, one can use data only up to a certain point to estimate the model, and then compare the model forecast for the time period withheld from the model with the actual data for that time period. Since a stress test is not a simple forecast but a prediction conditional on a scenario, another option is to construct forecasts that are conditional on the realized values of the macroeconomic variables in the time period withheld from the model. Generally, there is no reason to believe that a model that performs well in-sample will also perform well out-of-sample. In fact, there is a tradeoff. In-sample model fit tends to improve as the number of explanatory variables increases, while the precision of out-of-sample forecasts tend to deteriorate if there are too many factors.
Figure 2 shows the out-of-sample predictions of the default probability on home equity lines of credit, conditional on macroeconomic variables, for loan-level, county-level, and top-down models. In this case, we estimate all three models through January 2008 (denoted by the vertical line), after the initial increase in subprime mortgage default rates, but before the full-scale financial crisis. Based on the coefficients estimated on this time period, the forecast for the rest of sample is constructed as a function of actual macroeconomic variables. The figure clearly shows that the loan-level model (red line) fails to generate the high default probabilities that were actually observed at the peak of the crisis (black line). As discussed previously, this is due to the low sensitivity of the model to macroeconomic variables. The county-level model (green line) seems to match actual data more closely, while the top-down model (blue dashed line) overpredicts losses.
Figure 2
Out-of-sample predictions for default probability
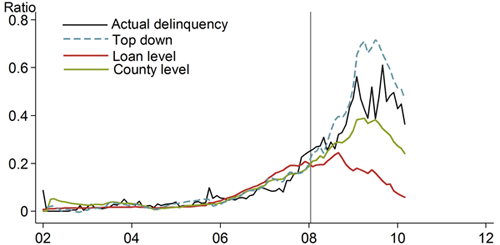
One concern is that these results reflect model specifications selected at each level of aggregation. To alleviate this concern, Hale, Krainer, and McCarthy (2015) estimate about 20 variations of the model specifications for each level of aggregation. They find that, across all these permutations, the out-of-sample fit of the county-level model is superior to that of loan-level or top-down models. While top-down models produce higher losses on average, which is generally viewed as a good thing for stress testing purposes, small changes in specification of these models could lead to large changes in the forecast errors, making these models less reliable.
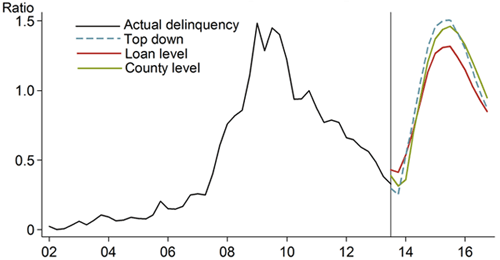
How much difference would this make in terms of actual stress testing? If models are estimated through the end of 2013 and then predictions are constructed for nine quarters ahead using the severely adverse scenario provided by the Federal Reserve for the 2014 Comprehensive Capital Analysis and Review (CCAR) exercise, this would mimic the modeling procedures that the banks had to do in January 2014. Figure 3 shows the predictions constructed from the models at the three levels of aggregation. Again, it is apparent that the loan-level model is not as sensitive as the others to stress. The loan-level default projection is quite a bit below the observed default rate in 2009, while county-level and top-down models come pretty close.
Figure 3
Model predictions of default
Conclusion
Hale, Krainer, and McCarthy (2015) demonstrate that for portfolios of home equity lines of credit, using intermediate levels of aggregation gives a model both stability and sufficient accuracy for stress testing. To glean some lessons from this analysis, it’s important to keep in mind a few caveats. First, stress testing is a very particular exercise in that both the inputs and the outputs are aggregates. Thus, while an intermediate level of aggregation is useful for stress testing, it might not be useful for other purposes like constructing internal loan ratings or developing appropriate loan pricing. Second, the specific level of aggregation that performs best might be different for different loan portfolios or across different institutions. Third, the choice is not limited to the three levels of aggregation discussed here. For example, if borrower creditworthiness changes substantially over time, aggregating the data according to consumer credit scores could accommodate such changes.
Therefore, we draw two general conclusions. First, when loan-level data are available, the level of aggregation should be considered in model development. In stress testing analysis especially, because both inputs and outputs are aggregate, one cannot simply assume that loan-level models are the best. Second, as a class, models estimated at an intermediate level of aggregation should receive more attention, as they can be useful for judging the accuracy of existing methodologies. Not only are they promising in terms of precise predictions and relative stability, they also tend to be relatively simple and easy to estimate.
Galina Hale is a research advisor in the Economic Research Department of the Federal Reserve Bank of San Francisco.
John Krainer is a research advisor in the Economic Research Department of the Federal Reserve Bank of San Francisco.
References
Hale, Galina, John Krainer, and Erin McCarthy. 2015. “Aggregation Level in Stress Testing Models” FRB San Francisco Working Paper 2015-14, September.
Frame, W. Scott, Kristopher Gerardi, and Paul S. Willen. 2015. “The Failure of Supervisory Stress Testing: Fannie Mae, Freddie Mac, and OFHEO.” FRB Atlanta Working Paper 2015-3 (March).
Hirtle, Beverly, Anna Kovner, James Vickery, and Meru Bhanot. 2015. “Assessing Financial Stability: The Capital and Loss Assessment under Stress Scenarios (CLASS) Model.” FRB New York Staff Report 663.
Opinions expressed in FRBSF Economic Letter do not necessarily reflect the views of the management of the Federal Reserve Bank of San Francisco or of the Board of Governors of the Federal Reserve System. This publication is edited by Anita Todd and Karen Barnes. Permission to reprint portions of articles or whole articles must be obtained in writing. Please send editorial comments and requests for reprint permission to research.library@sf.frb.org