Do Adjustment Lags Matter for Inflation-Indexed Bonds?

Several countries issue government-guaranteed bonds with cash flows that adjust with price inflation. These so-called inflation-indexed bonds include U.S. Treasury Inflation-Protected Securities (TIPS) and U.K. index-linked gilts. Typically, the price index used for the inflation adjustment tracks the prices of a representative basket of consumption goods. The cash flows of U.S. TIPS are adjusted with the all-items consumer price index (CPI), while U.K. index-linked gilts are adjusted with the retail prices index (RPI). As a result, such bonds deliver a real return as opposed to the nominal returns offered by conventional bonds with fixed coupon and principal payments.

Since the cash flows of inflation-indexed bonds can only be adjusted with inflation after the designated statistical authority announces its price index data, the process leads to some practical questions: What is the appropriate lag to use in the inflation adjustment? And does that choice matter for bond prices? This issue is also important for researchers who want to understand the differences between yields for standard fixed versus inflation-indexed bonds, also known as inflation compensation.

In this Letter, I examine the price differentials between several pairs of similar U.K. index-linked gilts whose main distinguishing feature is that one bond has a three-month lag in indexation, while the other has an eight-month lag. After accounting for coupon differences and a slight maturity mismatch, I find that the prices of bonds with a three-month lag are statistically higher, although the difference is not economically meaningful as long as the bonds have several years to maturity. Since inflation-indexed bonds are typically issued with at least five years to maturity, the results suggest that the lag choice has little consequence for the service costs of inflation-indexed debt.

Historical background

The United Kingdom was the first country to introduce bonds that are adjusted to compensate for inflation, known as index-linked gilts, in 1981. Like other U.K. gilts they pay semi-annual coupons. Until 2005 all index-linked gilts had an eight-month lag in their inflation indexation. The only apparent advantage of choosing this lag length is that investors know the money value of the interest payment at the start of each six-month trading period, which simplifies calculating the accrued interest.

In 2005 the U.K. Debt Management Office overhauled its index-linked program. In addition to increasing the maximum maturity at issuance from roughly 35 years to more than 50 years, it decided to follow the lead of Canada and the United States and switch to a three-month lag in the inflation indexation of newly issued index-linked gilts, which by then had become the global standard. Gilts with both three-month and eight-month indexation lags have been trading simultaneously since then. Hence, the U.K. index-linked market offers an ideal natural experiment for studying how different lags of inflation compensation affect prices in index-linked bonds.

The U.K. index-linked gilt market

The maturity distribution of all U.K. index-linked gilts outstanding since 2000 is shown in Figure 1. Downward-sloping lines plot the remaining years to maturity for each gilt according to the date of issue. Seasoned gilts with an eight-month lag in inflation indexation are shown with green lines, while those issued since 2005 with a three-month lag are shown with blue lines. The darker dashed lines highlight four pairs of new (blue) and seasoned (green) gilts that are very close to each other in terms of remaining time to maturity. The four pairs provide an opportunity to examine the pricing differences between these bonds in greater detail.

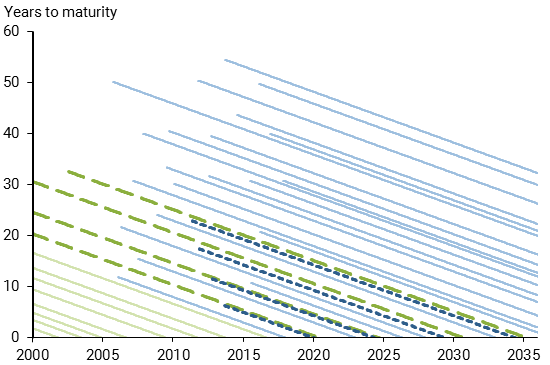
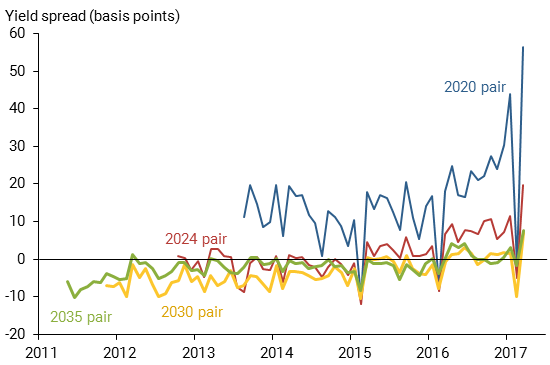
Figure 2 shows the yield spreads of these pairs beginning on the issue dates for each new gilt. The seasoned gilt in each pair matures in the years 2020, 2024, 2030, and 2035. As shown in Figure 1, the four new gilts have slightly shorter maturities than their seasoned counterparts, with the differences ranging from 3 to 15 months. The average yield spreads measured in hundredths of a percentage point, or basis points, are 15.2, 1.3, –3.6, and –1.9, respectively. Although the yield spreads can include both positive and negative values, they all trend upward over time. This is because the index-linked gilt yield curve is mostly upward-sloping, and the longer maturities of seasoned gilts should give them a higher yield, on average, and increasingly so as they approach maturity thanks to the greater steepness of the short end of the yield during the period shown.

To focus on the price differential in each pair, I control for all other factors, specifically differences in coupon sizes, the slight maturity mismatch, and the general shape of the yield curve. I assume that the bonds in each pair share similar liquidity risks, because index-linked gilts are generally illiquid and much less frequently traded than regular fixed-coupon gilts. It follows that any remaining price differences can be ascribed to the differences in the lag of their inflation indexation. To appropriately control for the listed factors, a model is needed.

The yield curve model

To capture the factors involved in the index-linked gilt yield curve, I use a model that describes the relationship between bond yields of different maturities, known as a term structure model. Specifically, I use the model introduced in Christensen, Diebold, and Rudebusch (2011), which incorporates three factors representing the general level of interest rates, the slope of the yield curve, and any humps in the shape of the yield curve.

My baseline hypothesis is that there is no material reason why investors such as pension funds should value bonds with a three-month lag in inflation compensation differently from those with an eight-month lag. This view is supported by Andreasen and Christensen (2016), who find that the compensation for risk that U.S. investors attach to inflation uncertainty, also known as the inflation risk premium, tends to be small at horizons less than 12 months; presumably, such short-term risk premiums are also small in the United Kingdom.

To produce a strong and very conservative test of this hypothesis, I estimate the yield curve model using only the prices of new index-linked gilts with the current three-month lag in indexation to make it as challenging as possible for the model to match the prices of the seasoned gilts with an eight-month lag. If this test were to succeed, it would suggest that there are, at most, small systematic differences in the prices between the two types of index-linked gilts.

Results

The model estimation measures the difference in yield to maturity between the actual and model-implied bond prices for new gilts, expressed as fitted errors in basis points. In addition, the model can be used to calculate the corresponding fitted errors for the seasoned gilt in each pair, even though their prices were not used in the model estimation. I then define the relative pricing error for each pair as the difference between the fitted error of the seasoned gilt and that of the new gilt. This result represents the residual effect of the differences in the inflation-indexation lag after controlling for differences in coupon sizes, maturity mismatches, and the shape of the yield curve.

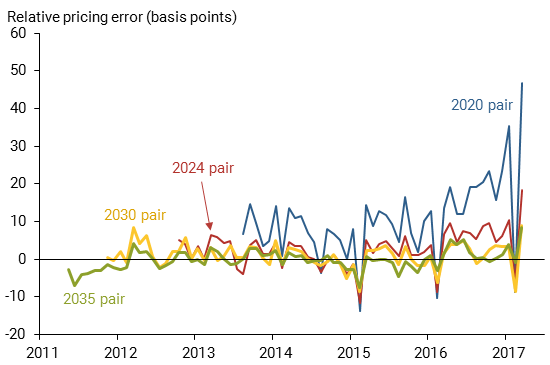
Figure 3 shows the relative pricing errors over time for all four pairs. The number of observations for each pair varies and is determined by the issuance date of the matching new gilt. The 2020 pair has 44 observations starting in August 2013, the 2024 pair has 54 observations starting in October 2012, the 2030 pair has 65 observations starting in November 2011, and the 2035 pair has 71 observations starting in May 2011. Based on a statistical test, the baseline hypothesis suggesting there is no difference in the average pricing errors between the newer and older gilts is rejected for all but the 2035 pair; the estimated average differences in basis points are 10, 3, 1, and 0, respectively, in favor of the new gilts. Although the average differences are statistically significant, only the 2020 pair that is closest to maturity is economically meaningful. For this pair, the pricing error for the seasoned gilt has quite a large seasonal variation in the early spring of each year, which is caused by seasonality in the underlying RPI. This pattern gets more pronounced as the security approaches maturity because differences in the exposure to the RPI seasonality are discounted over a shorter horizon.

To test the robustness of these results, I estimate the yield curve model with all index-linked gilts in the sample. This improves the model’s ability to match the prices of the seasoned gilts, but at the expense of its accuracy in matching the prices of the new gilts. In turn, this reduces the statistical differences in the model fit for the four gilt pairs quite notably. Thus, using all available information in the model makes it much harder to detect any systematic differences between the prices of the two types of gilts in each pair.

Conclusion

In this Letter, I analyze how differences in the lag of the cash flow adjustment for inflation-indexed bonds affect their prices. The results suggest that the lag length only matters as securities get close to maturity, when seasonality in the underlying price index plays a role. Given that governments tend to issue inflation-indexed bonds with a minimum of five years to maturity, this aspect of the contract does not seem to play a role for bond prices at the time of issuance. Because of this, the lag length should not matter for governments’ decisions about which types of inflation-indexed securities to issue. Furthermore, for researchers modeling real bond yields, the results suggest that limiting analysis to inflation-indexed bonds with at least five years to maturity as in, for example, Christensen, Lopez, and Rudebusch (2010), would not benefit much from refinements that account explicitly for the lag in inflation-indexation.

Jens H.E. Christensen is a research advisor in the Economic Research Department of the Federal Reserve Bank of San Francisco.

References

Andreasen, Martin M., and Jens H.E. Christensen. 2016. “TIPS Liquidity and the Outlook for Inflation.” FRBSF Economic Letter 2016-35 (November 21).

Christensen, Jens H.E., Francis X. Diebold, and Glenn D. Rudebusch. 2011. “The Affine Arbitrage-Free Class of Nelson-Siegel Term Structure Models.” Journal of Econometrics 164(1), pp. 4–20.

Christensen, Jens H.E., Jose A. Lopez, and Glenn D. Rudebusch. 2010. “Inflation Expectations and Risk Premiums in an Arbitrage-Free Model of Nominal and Real Bond Yields.” Journal of Money, Credit, and Banking 42(6, Supplement), pp. 143–178.