Standard asset price models have generally failed to detect bubbles, with enormous costs to the economy. Economists are now creating promising new models that account for bubbles by relaxing the assumption of rational expectations and allowing people’s decisions to be driven by their perceptions of what the future may hold. The following is adapted from a presentation by the president and CEO of the Federal Reserve Bank of San Francisco to the National Association for Business Economics in San Francisco, California, on September 9, 2013.
It’s a pleasure to be here at NABE’s 55th annual meeting. Your organization has done as much as any to support the profession and promote discussion of the most important economic questions of our time, so it’s a privilege to join you.
In my talk this morning, I will focus on an issue that has fascinated and perplexed economists for centuries—asset price bubbles. Obviously, the events of the past two decades demonstrate that this topic is not merely of academic interest. Asset price booms and busts distort the course of the economy and can leave enormous economic wreckage in their trail. In considering this topic, I’ll start by reviewing the basics of asset price theory. I’ll then highlight some striking inconsistencies between theory and evidence in standard models of asset prices. I’ll then explore some recently developed theories that may help explain why bubbles sometimes form and why they crash. And I’ll close with some speculation about the implications for monetary and macroprudential policy.
We economists like to explain things using highly stylized models. We build make-believe worlds, populate them with creatures that act according to strictly prescribed rules, and analyze what happens. Or, as my wife said after I described one of my research papers to her: “You really never did stop playing Dungeons and Dragons, did you?” The thing is, most of the time, this approach works remarkably well. Often, the simplest model—with patently unrealistic assumptions—yields the keenest insights into how a market or an economy works. Without doubt, Occam’s razor has proven to be a most valuable item in the economics toolkit.
Unfortunately, asset prices have proven less amenable to this kind of treatment. A cursory reading of the academic literature on asset prices reveals a litany of puzzles, conundrums, paradoxes, and anomalies. Much of the research on asset prices continues to rely on highly stylized models with identical agents, rational expectations, and optimizing behavior. According to the prevailing view, asset price surges that many would perceive to be bubbles are not really so. Instead, they are seen to reflect the influences of fundamental forces, such as a decline in risk appetite. This reminds me of the White Queen in Lewis Carroll’s Through the Looking-Glass (1871), who says jam will be given every other day, but never today. Adherents of this view may admit that bubbles have occurred in the past—like the dot-com boom and bust. And they may even be willing to accept that bubbles are something to worry about in the future—say, in financial supervision. But, in practice, they are never willing to find a bubble in the present. There’s always a reason why what looks like a bubble, walks like a bubble, and quacks like a bubble is not actually a bubble. But, as I’ll discuss in a moment, this is changing. Recent research not only recognizes that asset price bubbles really do form, but also holds great promise in unlocking their secrets and identifying them.
Let’s now consider standard asset price theory, according to which the price of an asset equals the discounted expected return of holding the asset for one period. For example, take a share in a corporation. The return consists of two parts: the dividend payment the owner receives and the capital gain or loss from selling the share. The same formula applies to owning a house or a bond, or any asset for that matter. For the house, the dividend payment is the service flow the owner derives from living in it or renting it out. For the bond, it is the coupon payment. According to this theory, three variables can affect asset prices: the discount factor, the dividend payment, and the expected future price appreciation.
It helps to simplify things a bit further. Under certain assumptions, including the absence of bubble-like behavior, Myron Gordon developed over 50 years ago an illuminating way of presenting this asset price formula. He noted that the ratio of the asset price to the dividend payment is inversely related to the difference between the expected future rate of return and the growth rate of inflation-adjusted dividends (Gordon 1959). That is, all else equal, the price-to-dividend ratio should be high when expected future dividend growth is high or when the expected future return to the asset is low. This is a classic case of an elegant and parsimonious theory. So, how does it stand up to the data?
Figure 1
Asset price booms and crashes
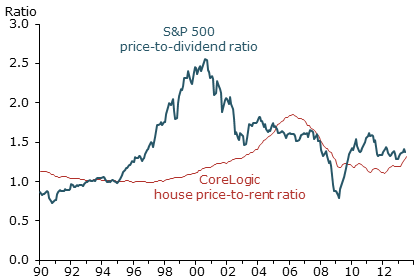
Note: Normalized to 1 in January 1995.
Sources: CoreLogic, BEA, and S&P 500 data from Shiller (2005, updated).
The first hurdle the model faces is the long history of boom and bust cycles in a variety of different asset prices. These were thoroughly documented by Robert Shiller (2005) in his book Irrational Exuberance. I’m an economist, so I need to show some numbers here. Figure 1 shows two well-known recent U.S. asset price booms and busts. The thick blue line shows the price-to-dividend ratio of the S&P 500 stock index from 1990 to the present. The thin red line shows the time series of the house price-to-rent ratio from the CoreLogic home price index, in which the rent data are the Bureau of Economic Analysis data on owners’ equivalent rent. In the stock market boom of the late 1990s, the price-to-dividend ratio rose over 100% in the five years up to the end of the boom in 2000. The recent housing boom was relatively tame by this standard. The house price-to-rent ratio climbed around 50% during the five years before the market peak in 2006. To put these numbers in perspective, according to flow of funds data, in the five years before they peaked, U.S. stock market wealth soared $12 trillion and housing wealth increased some $10 trillion.
What does the Gordon model have to say about these and other large surges in asset prices? Two explanations are possible based on changes in economic fundamentals. One is an upward shift in the expected growth rate of future dividends. The second is a reduction in investors’ expected returns on the asset. Importantly, in standard asset pricing theory, expectations of future dividend growth and future returns on assets are assumed to be rational. That is, expectations are assumed to be consistent with the structure of the model.
I’ll start with the first explanation, that a rise in the price-to-dividend ratio is caused by higher expected dividend growth. The evidence on this is clear and negative. With respect to U.S. stocks, over history, the price-to-dividend ratio is uncorrelated with future real dividend growth (Cochrane 2008). A similar pattern is seen with regard to the U.S. housing market. The price-to-rent ratio is uncorrelated with future real rent growth (Campbell et al. 2009 and Gelain and Lansing 2013). The international evidence is somewhat more mixed. But a recent cross-country study found that, in most countries, the correlation between the house price-to-rent ratio and future real rent growth is either statistically insignificant or has the opposite sign of that predicted by the theory (Engsted and Pedersen 2012). Indeed, in the most recent U.S. housing boom, the high house price-to-rent ratio observed during the boom did not foreshadow subsequent high real rent growth. In fact, the growth rate of real rents actually declined in the period following the peak price-to-rent ratio. It’s simply not the case that asset price movements can be explained by shifts in rational expectations of future dividend growth.
So that leaves the possibility that a lower expected return might be driving the increase in asset prices during a boom. The lower expected return could reflect a combination of lower alternative investment returns, say as measured by the general level of real interest rates, and/or a lower risk premium on the asset in question. As in the case of dividend growth, the evidence on expected future real interest rates driving asset prices is negative. Equity dividend-to-price ratios are generally not correlated with future changes in real interest rates (Campbell and Shiller 1988).
Thus, expectations of future dividends or real interest rates fail to explain asset price movements. Given that, standard approaches ascribe much of the variation in asset prices to movements in the discount factor used to compute the present value of future dividends. This is the logic of Sherlock Holmes in Arthur Conan Doyle’s The Sign of the Four (1890), who said that, “when you have eliminated the impossible, whatever remains, however improbable, must be the truth.” Time variation in the discount factor is the only remaining rational explanation. However, on their own, you can’t really judge whether movements in the discount factor are reasonable. After all, they are simply defined as the residual component of an identity implied by the theory. In this regard, the discount factor is akin to total factor productivity, which Moses Abramovitz (1956) famously described as “a measure of our ignorance.”
Moreover, the explanation that the discount factor is the main driver of movements in the price-to-dividend ratio has potentially falsifiable implications. In particular, it says that when the price-to-dividend ratio is high, rational investors should expect a relatively low rate of return on the asset. When valuations are low, rational expected returns should be high (Greenwood and Shleifer 2013). For example, if rational investors discount future dividends by less, perhaps owing to a reduction in risk aversion, then the price-to-dividend ratio rises and we see a boom in the asset price. And the expected future rate of return on the now higher-priced asset will be correspondingly lower.
Figure 2
Stock prices and investor optimism
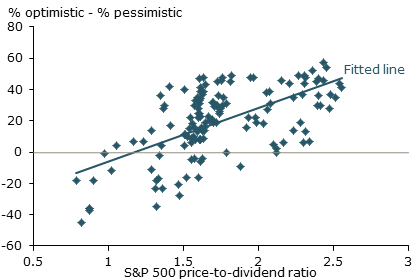
Sources: Greenwood and Shleifer (2013), Wells Fargo/Gallup, and S&P 500 data from Shiller (2005, updated). Thanks to the authors for supplying data used in this figure. Data are from 1996 to 2013.
So, are the data consistent with this prediction of the theory? One test is to compare real-world measures of investors’ expected returns with the expected returns implied by the theory. Fortunately, there are a number of surveys of investor expectations of future returns on stocks and houses that can be brought to bear on this question.
Let me jump to the bottom line. The evidence from surveys of investors’ expected returns is directly at odds with the implications of standard asset price theory. For one, stock market investors tend to expect high future returns when the price-to-dividend ratio is high, contrary to the theoretical prediction of a negative relationship between rational expected returns and the level of asset prices relative to dividends (Greenwood and Shleifer 2013). A picture tells the story. Figure 2 shows Gallup survey results on the relationship between the S&P 500 price-to-dividend ratio and investor optimism regarding stock market returns over the next year. Gallup asks whether people are optimistic, pessimistic, or neutral about future market returns. The figure reports the difference between the number saying they are optimistic or very optimistic and those saying they are pessimistic or very pessimistic. As the figure shows, periods of high stock valuations, such as the late 1990s and mid-2000s, are when investors were more optimistic regarding future stock gains. And during periods of relatively low valuations, such as the early 2000s and the period of the global financial crisis, investors had relatively low expectations of stock market returns. The positive relationship between current stock prices and expected future returns is consistent across a variety of surveys and alternative model specifications.
Figure 3
House prices and expected price appreciation
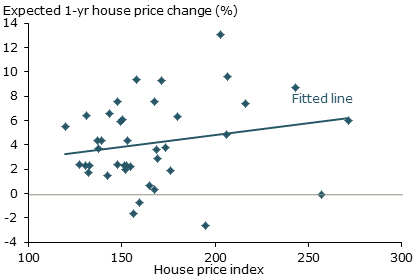
Sources: S&P/Case-Shiller, FHFA, and Case, Shiller, and Thompson (2012). Cities included are San Francisco/Alameda County, Boston, Los Angeles/Orange County, and Milwaukee. Data are from 2003 to 2012.
This same relationship is evident in data on house prices. Figure 3 plots the level of house prices and expected future house price appreciation in the United States over the past decade. Each data point represents one of four major cities in a given year (Case, Shiller, and Thompson 2012). The pattern is clear. Optimism about future house price appreciation tends to increase when house prices are high. Just as with stocks, the survey evidence directly contradicts the fundamental story that high house prices can be explained by a decline in the rational expected return from homeownership.
Let me sum up my points so far. According to standard asset price theory, an increase in asset prices must reflect either an increase in expected future dividend growth or a reduction in the expected return on the assets. We see large run-ups in equity and home prices. But they are not associated with higher future dividend growth rates or lower expected returns based on surveys. So far, this evidence is mainly destructive. But, in fact, a first step to understanding asset price bubbles can be found in the survey data I just discussed. The key is to relax the assumption of rational expectations and allow people’s decisions to be driven by their perceptions of what the future may hold.
Figure 4
Extrapolative expectations in the stock market
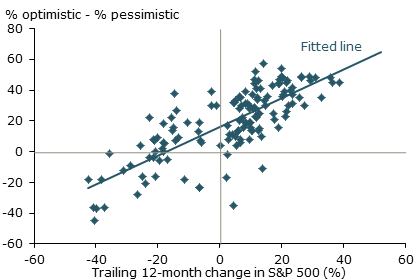
Sources: Greenwood and Shleifer (2013), Wells Fargo/Gallup, and S&P 500 data from Shiller (2005, updated). Thanks to the authors for supplying data used in this figure. Data are from 1996 to 2013.
A striking regularity seen in the survey data is that expectations of future gains are highly positively correlated with past observed returns. That is, despite the admonition that past performance is no guarantee of future results, people appear to assume exactly that in predicting future stock returns. Figure 4 shows the relationship between the Gallup survey of investor optimism about future stock market gains and the trailing 12-month change in the S&P 500 stock price index. The correlation is strongly positive. Indeed, the worst reading for the investor optimism index for the period shown in the figure occurred in early 2009, just as the stock market plunged to its recession low. And the highest reading of investor optimism occurred in early 2000, just before the tech stock crash. The evidence is compelling. People tend to extrapolate future stock price movements from recent stock price performance. This finding is confirmed by econometric analysis that uses different measures of investor expectations and controls for various other factors (Greenwood and Shleifer 2013).
The same dynamic of extrapolative expectations also plays out in housing markets in the United States and abroad. Figure 5 shows the relationship between expected house price appreciation over the next year from surveys and the percentage change in house prices observed over the prior year for four major U.S. cities over the past decade. As in the case of stock prices, the correlation is strongly positive. Figure 6 shows similar patterns for Norway and Sweden, two other countries that have experienced massive house price booms (Jurgilas and Lansing 2013). Just as in the United States, when house prices go up, people expect them to continue to rise. And when they fall, people turn much more pessimistic about future house price appreciation.
Figure 5
Extrapolative expectations in the housing market
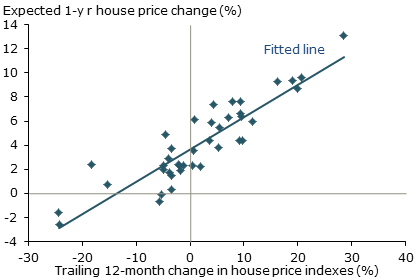
Sources: S&P/Case-Shiller, FHFA, and Case, Shiller, and Thompson (2012). Cities included are San Francisco/Alameda County, Boston, Los Angeles/Orange County, and Milwaukee. Data are from 2003 to 2012.
Figure 6
Scandinavia: House price expectations
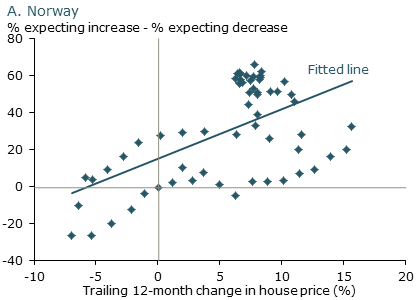
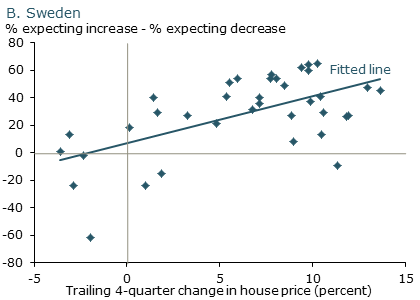
Source: Jurgilas and Lansing (2013). Data for Norway are from 2007 to 2012; data for Sweden are from 2003 to 2012.
Many researchers are probing why people have the procyclical pattern of optimism seen in these surveys. One key element in the theories coming out of this research is that people do not possess the full set of information assumed in the standard asset price model with rational expectations. Instead, they must make do with the limited information at hand when judging likely future discounted dividend payments and the future price of the asset. Indeed, a growing body of evidence in behavioral economics and finance shows that people’s expectations of future asset returns depend on their past experiences (Vissing-Jorgensen 2003 and Malmendier and Nagel 2011). This process of forecasting with limited information has been shown to cause forecast errors that can drive a wedge between asset prices and the values implied by economic fundamentals (Cutler, Poterba, and Summers 1991 and Barsky and DeLong 1993).
The recognition that people behave this way can move us a long way closer to understanding how asset price bubbles can emerge and how they can crash. To see this, let me return to the standard asset price formula. Recall that the price of an asset equals the value of its dividend plus the discounted value of the price at which you expect to be able to sell the asset. If one then assumes that investors’ expected price appreciation of the asset depends positively on its recent past price change, this introduces a positive feedback loop into asset price dynamics that is absent from the standard model assuming rational expectations. Indeed, a simple model of extrapolative expectations of future asset price movements does a very good job of explaining the big swings in the U.S. stock price-to-dividend ratio over time (Adam, Beutel, and Marcet 2013).
This principle has proven a good model of investor expectations. But a challenge to models based on extrapolative expectations is that they may create too much positive feedback in asset prices, producing excess volatility at odds with the data. Despite the failures of standard asset price theory, the price-to-dividend ratio is a good predictor of future excess returns on the stock market relative to the risk-free rate (Cochrane 2008). That is, a high price-to-dividend ratio today predicts relatively low average future stock returns. Therefore, for a model to succeed, it needs to allow for procyclical investor optimism, while incorporating a self-stabilizing mechanism that eventually stops and reverses this process, bringing prices back toward fundamental values. This is a delicate balance. One promising approach is to posit two types of traders, one with extrapolative expectations and the other that trades based on fundamentals (Cutler, Poterba, and Summers 1990 and Greenwood and Shleifer 2013). In a nutshell, the traders with extrapolative expectations drive the procyclical optimism, while the fundamental traders exert a stabilizing influence that keeps things from going completely off the rails (see Adam et al. 2013 for an alternative approach).
Researchers have yet to coalesce around one preferred model. However, a common theme in this literature is that the presence of a small amount of sand in the ability of people to process information can lead to large and sustained swings in asset prices, with significant repercussions for the economy. An important implication of these models is that nonfundamental asset price movements do not represent exogenous “shocks” to the economy. Rather, they are part of the endogenous behavior of the economic system. In particular, these asset price movements tend to amplify and propagate other shocks that occur within the system.
This recognition of the source of asset price movements means that work on monetary and macroprudential policies needs to refocus on how these policies may damp or amplify asset price cycles, rather than how they should respond to asset prices per se. For monetary policy, one implication of theories with endogenous asset price bubbles is that the time horizon over which policy affects the economy may be longer than typically thought. In particular, the policy response to cyclical movements in economic activity and inflation may have effects on investor beliefs and the behavior of asset prices that reach well into the future.
The lesson from history is clear: asset price bubbles and crashes are here to stay. They appear to be a consequence of human nature (Kindleberger 1978). And the events of the past decade demonstrate the enormous human costs of asset price bubbles and crashes.
To understand the past and avoid a recurrence of the devastating events we lived through so recently, we need to acknowledge that investors and financial markets do not behave the way rational asset price theory implies. We need to incorporate these channels into the models we use for forecasting, risk analysis, and policy evaluation. This opens up a world where actions, including regulatory and monetary policy measures, may have unintended consequences—such as excessive optimism, risk taking, and the formation of bubbles—that are assumed away in standard rational models.
Of course, this is a difficult task, and successful models are likely to be far more complicated than the simple and elegant rational models we have relied on in the past. But, it’s essential if we want to design policies that foster robust economic performance in the future.
References
Abramovitz, Moses. 1956. “Resource and Output Trends in the United States since 1870.” American Economic Review 46(2), pp. 5–23.
Adam, Klaus, Johannes Beutel, and Albert Marcet. 2013. “Stock Price Booms and Expected Capital Gains.” Unpublished manuscript, University of Mannheim.
Barsky, Robert B., and J. Bradford DeLong. 1993. “Why Does the Stock Market Fluctuate?” Quarterly Journal of Economics 108(2), pp. 291–311.
Campbell, Sean D., Morris A. Davis, Joshua Gallin, and Robert F. Martin. 2009. “What Moves Housing Markets: A Variance Decomposition of the Rent-Price Ratio.” Journal of Urban Economics 66(2), pp. 90–102.
Campbell, John Y., and Robert J. Shiller. 1988. “The Dividend-Price Ratio and Expectations of Future Dividends and Discount Factors.” Review of Financial Studies 1(3), pp. 195–228.
Case, Karl E., Robert J. Shiller, and Anne Thompson. 2012. “What Have They Been Thinking? Home Buyer Behavior in Hot and Cold Markets.” NBER Working Paper 18400.
Cochrane, John H. 2008. “The Dog That Did Not Bark: A Defense of Return Predictability.” Review of Financial Studies 21(4), pp. 1,533–1,575.
Cutler, David M., James M. Poterba, and Lawrence H. Summers. 1990. “Speculative Dynamics and the Role of Feedback Traders.” American Economic Review 80(2), pp. 63–68.
Cutler, David M., James M. Poterba, and Lawrence H. Summers. 1991. “Speculative Dynamics.” Review of Economic Studies 58(3), pp. 529–546.
Engsted, Tom, and Thomas Q. Pedersen. 2012. “Predicting Returns and Rent Growth in the Housing Market Using the Rent-to-Price Ratio: Evidence from the OECD Countries.” CREATES Research Paper 2012-58.
Gelain, Paolo, and Kevin J. Lansing. 2013. “House Prices, Expectations, and Time-Varying Fundamentals.” Federal Reserve Bank of San Francisco Working Paper 2013-03, February.
Gordon, Myron J. 1959. “Dividends, Earnings, and Stock Prices.” Review of Economics and Statistics 41(2), pp. 99–105.
Greenwood, Robin, and Andrei Shleifer. 2013. “Expectations of Returns and Expected Returns.” NBER Working Paper 18686.
Jurgilas, Marius, and Kevin J. Lansing. 2013. “Housing Bubbles and Expected Returns to Homeownership: Lessons and Policy Implications.” Forthcoming in Property Prices and Real Estate Financing in a Turbulent World, eds. M. Balling and J. Berg. Brussels: Société Universitaire Européenne de Recherches Financières (SUERF).
Kindleberger, Charles P. 1978. Manias, Panics, and Crashes: A History of Financial Crises. New York: Basic Books.
Malmendier, Ulrike, and Stefan Nagel. 2011. “Depression Babies: Do Macroeconomic Experiences Affect Risk-Taking?” Quarterly Journal of Economics 126(1), pp. 373–416.
Shiller, Robert J. 2005. Irrational Exuberance. 2nd edition. Princeton, NJ: Princeton University Press.
Vissing-Jorgensen, Annette. 2003. “Perspectives on Behavioral Finance: Does ‘Irrationality’ Disappear with Wealth? Evidence from Expectations and Actions.” Chapter in NBER Macroeconomics Annual 2003, Volume 18, eds. Mark Gertler and Kenneth Rogoff. Cambridge, MA: MIT Press, pp. 139–208.
Opinions expressed in FRBSF Economic Letter do not necessarily reflect the views of the management of the Federal Reserve Bank of San Francisco or of the Board of Governors of the Federal Reserve System. This publication is edited by Anita Todd and Karen Barnes. Permission to reprint portions of articles or whole articles must be obtained in writing. Please send editorial comments and requests for reprint permission to research.library@sf.frb.org