Insurance companies write policies to cover potential risks far into the future. Because the life of these contracts can extend well beyond the 30-year maturities for the longest U.S. Treasuries, it’s difficult to measure the interest rate risk involved. A new study describes how the long-term interest rates required to evaluate such long-lived liabilities can be extrapolated from shorter-maturity bond yields using a standard yield curve model. These extrapolations are a useful tool since they have very small errors relative to the yield curve variation typically considered for risk management.
A simple way to view interest rates is as the price you pay to be able to use money sometime in the future. Because U.S. Treasury securities are relatively risk free, their implied rates can be used to evaluate expected cash flows from other assets and liabilities. The longest maturity for Treasury bonds is 30 years, although some longer ones were issued in the past (Garbade 2017a, b). While this lifespan is sufficient for assessing many standard transactions, such as home mortgages, it’s hard to estimate what risk-free rates might be used for longer contracts.
Addressing this question is especially relevant for insurance companies. Like all financial firms, insurers are subject to interest rate risk, defined as fluctuations in the value of their assets and liabilities just from changes in the interest rates they are exposed to. However, the structure of their balance sheets is quite different from that of standard banks funded by deposits. Insurance liabilities are largely composed of promises to pay if specific life events occur in the future, such as a disability or death. Because these claims aren’t expected for many years, their effective maturity can be very long relative to the assets the companies hold. Thus, insurance firms can be exposed to risk from changes in longer-term interest rates. How might such risk be estimated to use in pricing longer-term assets and liabilities?
In this Letter, we describe our recent research, Christensen, Lopez, and Mussche (2017), assessing how reliably a well-established model, known as a dynamic term structure model, can extrapolate longer-term bond yields beyond the maximum maturity. Using this method to simulate yield curves, we find that the bias caused by the model extrapolations is quite small and inconsequential for managing interest rate risk. That is, the average extrapolation errors are much smaller than the yield curve variation needed to generate stress test scenarios used to measure how well institutions respond to risks from unknown future interest rates. Our findings suggest that the standard model-based approach using the existing Treasury yield curve is a reliable way to measure interest rate risk in the very long term.
Modeling the yield curve
A key component of financial transactions is calculating the present value of future cash flows. A common way to project that in the United States is by using the yield curve implied by rates on risk-free Treasury securities. However, since the longest securities mature in 30 years, what interest rates can be used for longer-term obligations, such as long-lived insurance liabilities? To solve this, we propose extrapolating the Treasury yield curve from a standard model based on the work of Nelson and Siegel (1987). Because this model’s yield curves have proven to be accurate in a wide variety of interest rate environments, it is widely used in research, particularly in its dynamic version described in Diebold and Li (2006), referred to as the dynamic Nelson-Siegel (DNS) model. The model’s three factors represent the general level of interest rates, the slope of the yield curve, and any humps or curvature in the shape of the yield curve. The DNS model allows the factors to adjust over time to account for relevant macroeconomic and market developments. Its main disadvantage is that it does not rule out arbitrage trading opportunities, but it fits bond data well, and such risks appear limited in practice.
To demonstrate how the DNS model can be used to measure longer-term interest rate risk, Christensen, Lopez, and Mussche (2017) examine yield curves from various countries; the larger study finds that the DNS model provides accurate extrapolations of long-term yields relative to alternative models. For this Letter, we focus on a sample of U.S. Treasury bond yields with 11 maturities ranging from 3 months up to 30 years covering the 20-year period from January 1995 to October 2016. We use data based on the work of Gürkaynak, Sack, and Wright (2007). The yield curve fitted to the data can then be extrapolated to generate the longer-term yields required; that is, the model estimates of three yield curve factors are used to extrapolate yields beyond the 30-year maturity available in the data out to the 50-year maturity we are examining.
Figure 1 shows the observed and fitted Treasury yield curves up to the 30-year maturity and the extrapolated long-term yields implied by the DNS model as of the last day in our sample, October 14, 2016. The fitted part of the yield curve is shown with a solid line, while the extrapolation is shown with a dashed line. We note that the extrapolated portion is relatively flat, which is consistent with the longer-term interest rates observed for European government bonds with maturities up to 50 years. This feature of the DNS model may be comforting to market practitioners since anecdotal evidence suggests that pricing of illiquid long-term bonds in, say, the corporate bond market often simply extrapolates the longest observed rate as a constant, a practice referred to as “flat forwards” among bond traders.
Figure 1
Observed, fitted, and extrapolated Treasury yields
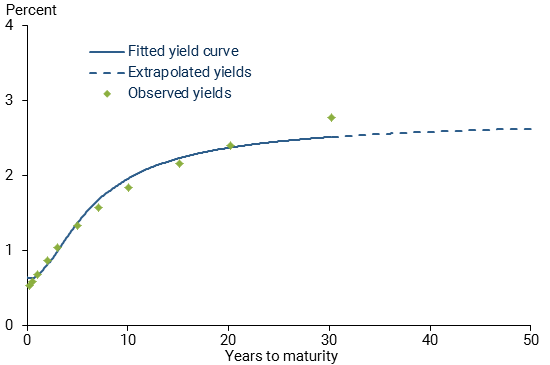
Note: Based on data as of October 14, 2016.
Simulation study
A standard approach to assessing the model-based extrapolations in these circumstances is to analyze specific simulations to see how the model performs on simulated data whose properties we already know. To study whether long-term yields extrapolated from the DNS model are reliable, we simulate yield samples from three different models that, unlike the DNS model, preclude the existence of arbitrage opportunities in the bond market. The first model is an arbitrage-free yield curve model with the standard three factors (level, slope, and curvature) and a constant volatility driving the data innovations; we call this the CV model. The second model introduces time-varying (or stochastic) volatility of these innovations by linking it to the model’s level factor; we call this the SV model. The third model introduces additional slope and curvature factors that address potentially different behavior in the long end of the yield curve; we call this five-factor model the GCV model. See Christensen et al. (2017) for more details.
We generate 100 samples of yield curves from each model at a monthly frequency for a 10-year period with maturities ranging from 3 months up to 50 years. From these simulated yield curves, we use yields with maturities up to 30 years as input data for the DNS model estimations so we can quantify the size of the extrapolation error for 50-year yields.
Using simulated data from the CV model, the extrapolation error from the DNS model for the 50-year yield averages –0.24% (24 basis points). Note that a negative sign means the model overstates the 50-year yield. The simulations from the SV and GCV models have smaller average extrapolation errors of 3 and 13 basis points, respectively, although their ranges of errors are wider. Thus, although different across simulation samples, the average extrapolation errors for 50-year yields are small and not much larger than the fitted errors from our 30-year yield sample.
Simulated yield projections
Our simulation results suggest that the DNS model can project long-term interest rates reasonably well on average. Next we consider how widely yields generated by the DNS model vary, which is a central point for interest rate risk management. This is also key for generating adverse scenarios for stress tests (Christensen, Lopez, and Rudebusch 2014 and Christensen and Lopez 2015). To give a sense of the yield variation and put the extrapolation bias into context, we follow the approach of Christensen, Lopez, and Rudebusch (2015) and generate 10,000 yield curve simulations over a three-year horizon using the DNS model estimated as of the last day of our sample.
We focus on the simulated paths for the 10-year Treasury yield, which is a key benchmark for all financial institutions, but note that the results for the 50-year yields are qualitatively similar. Figure 2 shows the median and the range for the central 90% of the outcomes for the 10-year yield from the simulated interest rate scenarios. The median rate indicates a continued gradual increase in the long-term interest rate, consistent with current market projections. The upper 95th percentile (top dashed line) rises more rapidly and reaches 5% after three years, while the lower 5th percentile (bottom dashed line) returns to the very low interest rate environment that prevailed in the years immediately after the financial crisis.
Figure 2
Simulated 10-year yield projections as of October 14, 2016
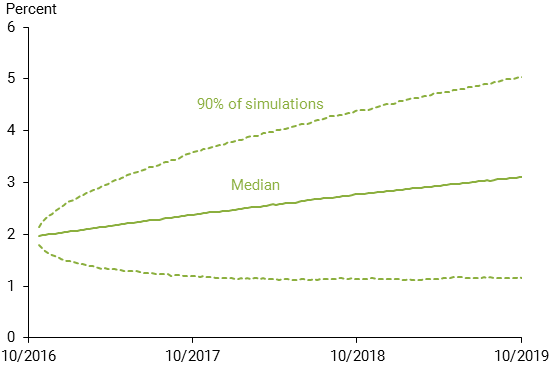
Figure 3 shows the entire yield curves corresponding to these three percentiles of 10-year yield projections for October 2019. Note the shape of the estimated yield curves vary widely over the next three years, up to 400 basis points or 4 percentage points apart. This underscores that the DNS model can generate a wide range of yield outcomes, even at the relatively short projection horizons typically considered in regulatory stress tests of financial institutions.
Figure 3
Simulated yield curves beginning in October 2019
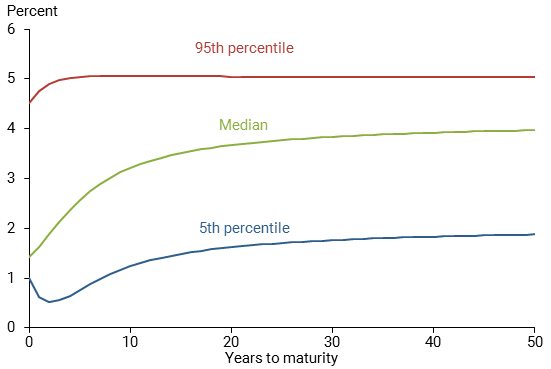
This dispersion provides a reasonable range of outcomes for stress testing and for interest rate risk management more generally. The extrapolation bias of 24 basis points from the DNS model is a fraction of the total variation the model generates and is not likely to meaningfully influence any conclusions drawn from the extrapolated yields. Thus, the model-implied longer-term yields should be acceptable for measuring longer-term interest rate risk.
Conclusion
In this Letter, we analyze a well-established yield curve model’s ability to extrapolate bond yields for longer maturities than are currently available for securities. Based on simulations from three alternative models, we find that our preferred model performs well at extrapolating long bond yields up to a maturity of 50 years using data with maturities up to only 30 years. More importantly, we show that any extrapolation errors are dwarfed by the variation in yield curve outcomes that the model generates. Thus, these small errors do not materially undermine the model’s usefulness as a risk measurement tool for longer-term interest rate risk exposure, such as in insurance company liabilities.
Jens H. E. Christensen is a research advisor in the Economic Research Department of the Federal Reserve Bank of San Francisco.
Jose A. Lopez is a vice president in the Economic Research Department of the Federal Reserve Bank of San Francisco.
Paul L. Mussche is a senior quantitative risk specialist in the risk modeling research unit of the Financial Supervision and Credit Department of the Federal Reserve Bank of San Francisco.
References
Christensen, Jens H.E. and Jose A. Lopez. 2015. “Assessing Supervisory Scenarios for Interest Rate Risk.” FRBSF Economic Letter 2015-29 (September 8).
Christensen, Jens H.E., Jose A. Lopez, and Paul L. Mussche. 2017. “Model-Based Extrapolation of Bond Yields.” Manuscript, FRB San Francisco.
Christensen, Jens H.E., Jose A. Lopez, and Glenn D. Rudebusch. 2014. “Stress Testing the Fed.” FRBSF Economic Letter 2014-08 (March 24).
Christensen, Jens H.E., Jose A. Lopez, and Glenn D. Rudebusch. 2015. “A Probability-Based Stress Test of Federal Reserve Assets and Income.” Journal of Monetary Economics 73, pp. 26–43.
Diebold, Francis X., and Canlin Li. 2006. “Forecasting the Term Structure of Government Bond Yields.” Journal of Econometrics 130, pp. 337–364.
Garbade, Kenneth D. 2017a. “Beyond 30: Long-Term Treasury Bond Issuance from 1953 to 1957.” Liberty Street Economics, February 6.
Garbade, Kenneth D. 2017b. “Beyond 30: Long-Term Treasury Bond Issuance from 1957 to 1965.” Liberty Street Economics, February 8.
Gürkaynak, Refet S., Brian Sack, and Jonathan H. Wright. 2007. “The U.S. Treasury Yield Curve: 1961 to the Present.” Journal of Monetary Economics 54(8), pp. 2,291–2,304.
Nelson, Charles R., and Andrew F. Siegel. 1987. “Parsimonious Modeling of Yield Curves.” Journal of Business 60(4), pp. 473–489.
Opinions expressed in FRBSF Economic Letter do not necessarily reflect the views of the management of the Federal Reserve Bank of San Francisco or of the Board of Governors of the Federal Reserve System. This publication is edited by Anita Todd and Karen Barnes. Permission to reprint portions of articles or whole articles must be obtained in writing. Please send editorial comments and requests for reprint permission to research.library@sf.frb.org