Stock Market Valuation and the Macroeconomy

Making judgments about the appropriate level of stock prices is a difficult and often humbling endeavor. One valuation metric, the cyclically adjusted price-earnings or CAPE ratio for the Standard & Poor’s (S&P) 500 stock index was originally developed by Campbell and Shiller (1998) to help judge whether the stock market is overvalued. The CAPE ratio is computed as the real, that is, inflation-adjusted, value of the S&P 500 divided by the real earnings of companies in the index averaged over the most recent 10 years. Campbell and Shiller found that higher values of the CAPE ratio predicted lower future real returns on stocks over subsequent 10-year periods. As noted in Siegel (2016), the CAPE ratio “has served as one of the best forecasting models for long-term future stock returns.”

This Economic Letter examines whether the current elevated level of the CAPE ratio can be justified by the prevailing macroeconomic environment. A parsimonious set of macroeconomic variables can account for much of the movement in the CAPE ratio over the past five decades. These variables include the “natural” real rate of interest, the growth rate of potential GDP, and the core inflation rate. Reasonable projections for these same macroeconomic variables over the next 10 years can provide a prediction about future movements in the CAPE ratio, which, in turn, will influence the magnitude of future stock returns.

The CAPE ratio in historical perspective

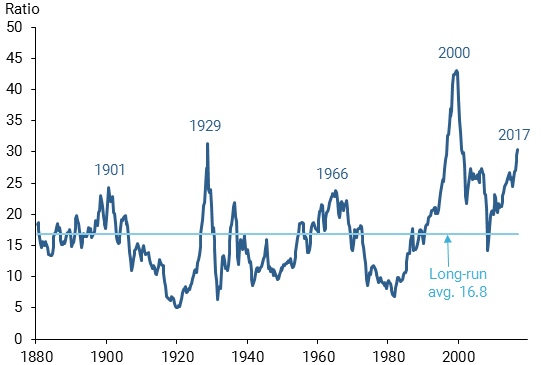
Figure 1 plots the CAPE ratio from 1881 to 2017; it shows five major stock price run-ups, including the most recent one that began in March 2009. Shiller (2000) argues that each of the first four run-ups coincided with the emergence of a “new era theory” in the popular culture that extolled the virtues of new technologies. The resulting investor enthusiasm fueled a “this time is different” mentality in which traditional valuation metrics were ignored, causing stocks to become overvalued relative to earnings. The exciting new technologies at the time included high-speed rail travel (early 1900s), automobiles and commercial radio (1920s), television and space travel (1960s), and the Internet (late 1990s). Stock price surges during each of these episodes pushed the CAPE ratio well above its long-run average. Each surge was followed by a substantial decline in stock prices that eventually pushed the ratio below its long-run average.

At the end of the most recent data sample in 2017:Q3, the quarterly average CAPE ratio stands at around 30, exceeded only by the peak values of 43 in 2000 and 31 in 1929. Possibly taking note of this situation, the minutes of the June 13–14, 2017, Federal Open Market Committee (FOMC) meeting stated that “in the assessment of a few participants, equity prices were high when judged against standard valuation measures” (Board of Governors 2017a). But in contrast, the minutes of the July 25–26, 2017 FOMC meeting stated that a “couple of participants noted that favorable macroeconomic factors provided backing for current equity valuations” (Board of Governors 2017b).

The CAPE ratio and macroeconomic variables

Before labeling the latest run-up in the CAPE ratio as another speculative bubble, it’s worth considering whether the current elevated value can be explained by “favorable macroeconomic factors.” In theory, the fundamental price of a stock is determined by the present value of expected future earnings distributions, or cash flows, that accrue to shareholders. The discount rate used in the present value calculation is composed of a risk-free rate of return and compensation for perceived risk, called a risk premium. All else being equal, a lower risk-free rate or a lower risk premium would imply that future cash flows are discounted less, causing the fundamental price to rise. Another variable that can influence the fundamental price is the expected growth rate of future cash flows, with higher growth implying a higher price.

One measure of the risk-free rate of return is the natural rate of interest, or r-star (r*). This is the inflation-adjusted, short-term interest rate that is consistent with the full use of economic resources and steady inflation near the central bank’s target level. Standard economic models imply that r-star is linked to households’ degree of patience, which influences their willingness to save, and to the expected growth rate of potential GDP, which influences the rate of return from saving. The same models imply that the growth rate of potential GDP determines the long-run growth rate of real cash flows from stocks.

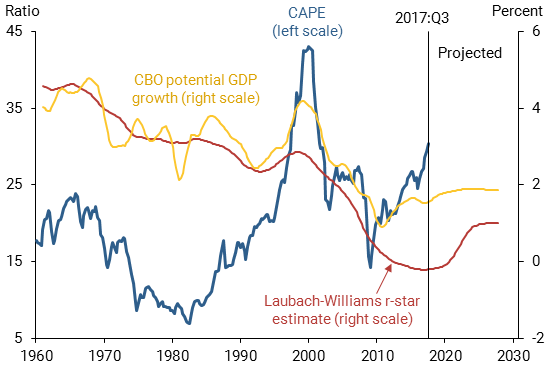
Figure 2 shows the relationship between the CAPE ratio, an estimate of r-star, and the four-quarter growth rate of potential GDP. The r-star series is the two-sided estimate from Laubach and Williams (2016); the potential GDP series is from the Congressional Budget Office (CBO). The CAPE ratio exhibits a mostly upward-sloping trend, particularly since the early 1980s. R-star and potential GDP growth both exhibit downward-sloping trends, but the decline in r-star is more pronounced. Beyond the end of the data sample, potential GDP growth can be projected forward 10 years using CBO estimates. Similar to the methodology in Lansing (2016), the historical statistical relationship between potential GDP growth and r-star can be used to construct a 10-year projection for the natural rate of interest. The CBO’s projection of a gradual rise in potential growth over the next 10 years implies a gradual rise in r-star to a value around 1%.

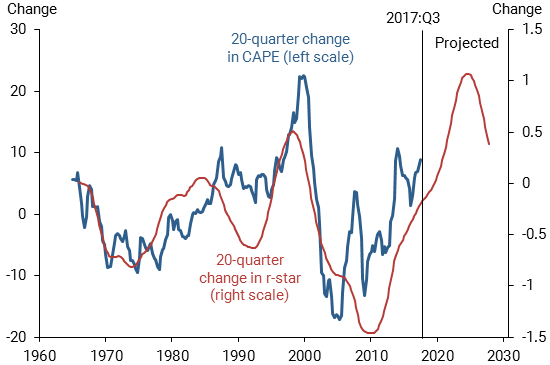
While r-star and the CAPE ratio appear to move in opposite directions over the longer run, some additional insight can be gained by examining shorter-run movements, say over 5 years, or 20 quarters. Figure 3 shows that shorter-run movements in r-star generally go in the same direction as the CAPE ratio. The correlation between the two series is strongly positive. This pattern is consistent with the idea that upward movements in r-star tend to be observed during booms or recoveries, which are periods of lower macroeconomic uncertainty (Lansing 2017). Lower uncertainty stimulates investors’ demand for risky assets like stocks, contributing to a rise in the CAPE ratio. Likewise, downward movements in r-star tend to be observed during recessions or crises, which are periods of higher uncertainty. Higher uncertainty stimulates investors’ demand for safe assets like U.S. Treasury securities while stock prices tend to fall, contributing to a decline in the CAPE ratio. Using the projected path for r-star from Figure 1, the projected path for the 20-quarter change in r-star shows a continued increase for a time, followed by a reversal as r-star levels off at 1%.

The numerator and denominator of the CAPE ratio are both adjusted for inflation. Despite this feature, the correlation coefficient between the CAPE ratio and inflation is strongly negative. This pattern is consistent with a theory that stock investors fail to properly account for inflation in their present value calculations, causing stocks to become undervalued during periods of high inflation and overvalued during periods of low inflation. This type of mispricing could occur if stock investors adjust their discount rate in response to inflation-induced shifts in the prevailing nominal interest rate but, for some unexplained reason, they fail to make similar inflation adjustments to the expected growth rate of future nominal cash flows (Lansing 2004).

The four-quarter change in the core personal consumption expenditures (PCE) price index, which removes volatile food and energy prices, is currently around 1.4%. A reasonable projection is that this measure of inflation will rise gradually to reach the FOMC’s 2% target.

Fitted and projected values for the CAPE ratio

A simple regression model can be used to assess how well macroeconomic variables explain movements in the CAPE ratio. Specifically, the model regresses the quarterly average CAPE ratio on a constant, the Laubach-Williams (LW) two-sided estimate of r-star, the CBO four-quarter growth rate of potential GDP, the 20-quarter change in the LW r-star estimate, and the four-quarter core PCE inflation rate. The explanatory variables are each lagged by one quarter in the regression equation to help account for real-time data availability issues.

Figure 4 plots fitted values of the CAPE ratio from the regression model through 2017:Q3. The fit is quite good, accounting for 70% of the variance in the actual CAPE ratio over the past five decades. All of the explanatory variables are statistically significant. The estimated coefficients on r-star and inflation are negative, while the estimated coefficients on potential GDP growth and the 20-quarter change in r-star are positive. At the end of the data sample, the actual CAPE ratio is about 8% above the fitted ratio. In contrast, the actual ratio is about 40% above the fitted ratio in early 2000, corresponding to the peak of the Internet bubble. Hence, compared with the previous bubble episode, the current elevated value of the CAPE ratio appears far less anomalous in light of the prevailing macroeconomic environment.

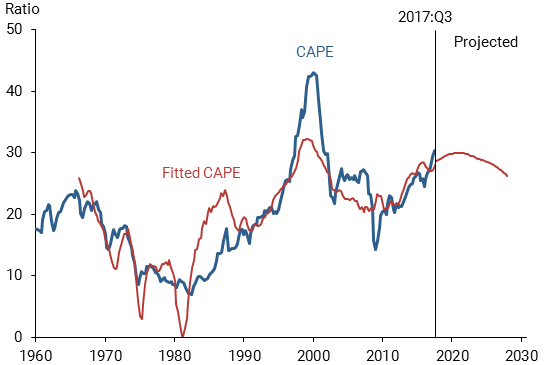
Inserting the 10-year projected paths for the macroeconomic variables into the regression equation yields a 10-year projected path for the CAPE ratio. The projected ratio initially rises then falls, ending up at 26.3—about 13% below the actual value at the end of the data sample. It’s worth contemplating the implications of a 13% decline in the CAPE ratio over the next 10 years. The extraordinary returns on stocks recorded since the market bottom in March 2009 have been driven in large part by the approximate doubling of the CAPE ratio. Absent further changes in the ratio, stock prices can rise only as fast as earnings. Over the past 30 years, real earnings for the S&P 500 have grown at an average compound rate of about 4% per year. A decline in the CAPE ratio from current levels would imply that stock prices must grow slower than earnings. All else being equal, stock returns in this case would be lower than those observed since 2009 when the CAPE ratio was doubling. Investors who expect high stock returns in the coming years based on recent market experience may end up being disappointed.

Conclusion

Over the long history of the stock market, extreme run-ups in the CAPE ratio have signaled that stocks may be overvalued. A simple regression model that employs a parsimonious set of macroeconomic explanatory variables can account for most of the run-up in the CAPE ratio since 2009, offering some justification for its current elevated level. The same model predicts a 13% decline in the CAPE ratio over the next 10 years. This prediction, if realized, would imply lower returns on stocks relative to those enjoyed in recent years when the CAPE ratio was rising.

Kevin J. Lansing is a research advisor in the Economic Research Department of the Federal Reserve Bank of San Francisco.

References

Board of Governors of the Federal Reserve System. 2017a. “Minutes of the Federal Open Market Committee, June 13–14, 2017.” 

Board of Governors of the Federal Reserve System. 2017b. “Minutes of the Federal Open Market Committee, July 25–26, 2017.” 

Campbell, John Y., and Robert J. Shiller. 1998. “Valuation Ratios and the Long-Run Stock Market Outlook.” Journal of Portfolio Management 24(2), pp. 11–26.

Lansing, Kevin J. 2004. “Inflation-Induced Valuation Errors in the Stock Market.” FRBSF Economic Letter 2004-30 (October 29).

Lansing, Kevin J. 2016. “Projecting the Long-Run Natural Rate of Interest.” FRBSF Economic Letter 2016-25 (August 29).

Lansing, Kevin J. 2017. “R-star, Uncertainty and Monetary Policy.” FRBSF Economic Letter 2017-16 (May 30).

Laubach, Thomas, and John C. Williams. 2016. “Measuring the Natural Rate of Interest Redux.” Business Economics 51, pp. 257–267. Updated data available.

Shiller, Robert J. 2000. Irrational Exuberance. Princeton, NJ: Princeton University Press.

Siegel, Jeremy J. 2016. “The Shiller CAPE Ratio: A New Look.” Financial Analysts Journal 72(3), pp. 41–50.